以下问题皆是来自ProjectEuler.net的趣题。该文章会持续更新,直到你们的浏览器处理不过来……(Chrome/Chromium浏览器请小心)
点击题目ID可直接查看ProjectEuler.net上的原文,在ProjectEuler.net注册登录后便可提交你的答案。
另附上我翻译的一些题目的解答分析的PDF文件(来自Project Euler的英文文档)。
直接看答案或题目解答分析没乐趣的,总之遵从自愿原则。
问题分析PDF文件下载(前10题,有些式子打错了,我想大家能看出来的),点她→
目前共翻译372题。
~_~ 第202题的题目依然看不懂。看来得弄个数学方面的Web Font,不然Unicode字符问题真不好解决。
另外,下面的翻译有不少错漏的地方!!
最后,该页面的内容正在向 http://likelikeslike.com/projecteuler/ 迁移!!本页面不稳定,请及时保存!
如需更多更好的題目翻译,请至:https://pe-cn.github.io
All the following problems come from ProjectEuler.net
Problem 1
如果列出小于10的所有是3或5的倍数的自然数,有3丶5丶6和9,它们的和是23。
现在请你算出所有1000以下为3或5的倍数的自然数的和。
Problem 2
Fibonacci数列的每后一项都是前面两项的和,若开始的头两项是1和2,那么前10个项就是:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
请求出以上Fibonacci数列中不超过400,0000的所有偶数的和。
Problem 3
13195的质因数有5丶7丶13丶29。
问:600851475143的最大质因数是……?
Problem 4
假如一个数前后掉转后还是同一个数的话,那个数就叫做「回文数」。由两个二位数的积构成的最大回文数是9009 = 91 × 99。
请找出由两个三位数的积构成的最大回文数。
Problem 5
2520是能被1到10的自然数整除的最小正整数。
那么,能被1到20的自然数整除的最小正整数是……?
Problem 6
前十个正整数的平方和是:12 + 22 + ... + 102 = 385
前十个正整数的和的平方是:(1 + 2 + ... + 10)2 = 552 = 3025
因此前十个正整数的和的平方,与前十个正数整数的平方和,的差是2640。
现在请你求出前一百个正整数的和的平方与前一百个正整数的平方和的差。
Problem 7
通过列出前6个质数,我们可知第6个质数是13。
那么第10001个质数是多少呢?
Problem 8
你能够从以下的1000位的数字中,找出连续五位数的积,其积最大吗?
73167176531330624919225119674426574742355349194934
96983520312774506326239578318016984801869478851843
85861560789112949495459501737958331952853208805511
12540698747158523863050715693290963295227443043557
66896648950445244523161731856403098711121722383113
62229893423380308135336276614282806444486645238749
30358907296290491560440772390713810515859307960866
70172427121883998797908792274921901699720888093776
65727333001053367881220235421809751254540594752243
52584907711670556013604839586446706324415722155397
53697817977846174064955149290862569321978468622482
83972241375657056057490261407972968652414535100474
82166370484403199890008895243450658541227588666881
16427171479924442928230863465674813919123162824586
17866458359124566529476545682848912883142607690042
24219022671055626321111109370544217506941658960408
07198403850962455444362981230987879927244284909188
84580156166097919133875499200524063689912560717606
05886116467109405077541002256983155200055935729725
71636269561882670428252483600823257530420752963450
Problem 9
勾股数组就是三个自然数a, b, c:
例如,32 + 42 = 9 + 16 = 25 = 52。
现存在唯一的勾股数组a, b, c,且a + b + c = 1000。请求出这三个数的乘积。
Problem 10
10以下的质数的和为2 + 3 + 5 + 7 = 17。
请求出200,0000以下所有质数的和。
Problem 11
在以下20×20的方阵中,用红色标记了四个在同一斜线上的数字。
08 02 22 97 38 15 00 40 00 75 04 05 07 78 52 12 50 77 91 08
49 49 99 40 17 81 18 57 60 87 17 40 98 43 69 48 04 56 62 00
81 49 31 73 55 79 14 29 93 71 40 67 53 88 30 03 49 13 36 65
52 70 95 23 04 60 11 42 69 24 68 56 01 32 56 71 37 02 36 91
22 31 16 71 51 67 63 89 41 92 36 54 22 40 40 28 66 33 13 80
24 47 32 60 99 03 45 02 44 75 33 53 78 36 84 20 35 17 12 50
32 98 81 28 64 23 67 10 26 38 40 67 59 54 70 66 18 38 64 70
67 26 20 68 02 62 12 20 95 63 94 39 63 08 40 91 66 49 94 21
24 55 58 05 66 73 99 26 97 17 78 78 96 83 14 88 34 89 63 72
21 36 23 09 75 00 76 44 20 45 35 14 00 61 33 97 34 31 33 95
78 17 53 28 22 75 31 67 15 94 03 80 04 62 16 14 09 53 56 92
16 39 05 42 96 35 31 47 55 58 88 24 00 17 54 24 36 29 85 57
86 56 00 48 35 71 89 07 05 44 44 37 44 60 21 58 51 54 17 58
19 80 81 68 05 94 47 69 28 73 92 13 86 52 17 77 04 89 55 40
04 52 08 83 97 35 99 16 07 97 57 32 16 26 26 79 33 27 98 66
88 36 68 87 57 62 20 72 03 46 33 67 46 55 12 32 63 93 53 69
04 42 16 73 38 25 39 11 24 94 72 18 08 46 29 32 40 62 76 36
20 69 36 41 72 30 23 88 34 62 99 69 82 67 59 85 74 04 36 16
20 73 35 29 78 31 90 01 74 31 49 71 48 86 81 16 23 57 05 54
01 70 54 71 83 51 54 69 16 92 33 48 61 43 52 01 89 19 67 48
这四个数字的乘积是26 × 63 × 78 × 14 = 1788696。
请在上面的方阵中找出在同一条直线上的四个连续的数字,使其乘积最大。(直线方向可为上下丶左右或与水平线呈45度夹角)
Problem 12
「三角数」即用递增的自然数相加得到的数,因此第7个三角数为1 + 2 + 3 + 4 + 5 + 6 + 7 = 28。前10个三角数为:
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...
先让我们来看看前7个三角数各自都有哪些因数吧:
- 1: 1
- 3: 1,3
- 6: 1,2,3,6
- 10: 1,2,5,10
- 15: 1,3,5,15
- 21: 1,3,7,21
- 28: 1,2,4,7,14,28
可见,28是第一个拥有超过5个因数的三角数。
那么第一个拥有超过500个因数的三角数是……?
Problem 13
请计算出下面100个50位数字的和的(左数)前10位数字。
37107287533902102798797998220837590246510135740250
46376937677490009712648124896970078050417018260538
74324986199524741059474233309513058123726617309629
91942213363574161572522430563301811072406154908250
23067588207539346171171980310421047513778063246676
89261670696623633820136378418383684178734361726757
28112879812849979408065481931592621691275889832738
44274228917432520321923589422876796487670272189318
47451445736001306439091167216856844588711603153276
70386486105843025439939619828917593665686757934951
62176457141856560629502157223196586755079324193331
64906352462741904929101432445813822663347944758178
92575867718337217661963751590579239728245598838407
58203565325359399008402633568948830189458628227828
80181199384826282014278194139940567587151170094390
35398664372827112653829987240784473053190104293586
86515506006295864861532075273371959191420517255829
71693888707715466499115593487603532921714970056938
54370070576826684624621495650076471787294438377604
53282654108756828443191190634694037855217779295145
36123272525000296071075082563815656710885258350721
45876576172410976447339110607218265236877223636045
17423706905851860660448207621209813287860733969412
81142660418086830619328460811191061556940512689692
51934325451728388641918047049293215058642563049483
62467221648435076201727918039944693004732956340691
15732444386908125794514089057706229429197107928209
55037687525678773091862540744969844508330393682126
18336384825330154686196124348767681297534375946515
80386287592878490201521685554828717201219257766954
78182833757993103614740356856449095527097864797581
16726320100436897842553539920931837441497806860984
48403098129077791799088218795327364475675590848030
87086987551392711854517078544161852424320693150332
59959406895756536782107074926966537676326235447210
69793950679652694742597709739166693763042633987085
41052684708299085211399427365734116182760315001271
65378607361501080857009149939512557028198746004375
35829035317434717326932123578154982629742552737307
94953759765105305946966067683156574377167401875275
88902802571733229619176668713819931811048770190271
25267680276078003013678680992525463401061632866526
36270218540497705585629946580636237993140746255962
24074486908231174977792365466257246923322810917141
91430288197103288597806669760892938638285025333403
34413065578016127815921815005561868836468420090470
23053081172816430487623791969842487255036638784583
11487696932154902810424020138335124462181441773470
63783299490636259666498587618221225225512486764533
67720186971698544312419572409913959008952310058822
95548255300263520781532296796249481641953868218774
76085327132285723110424803456124867697064507995236
37774242535411291684276865538926205024910326572967
23701913275725675285653248258265463092207058596522
29798860272258331913126375147341994889534765745501
18495701454879288984856827726077713721403798879715
38298203783031473527721580348144513491373226651381
34829543829199918180278916522431027392251122869539
40957953066405232632538044100059654939159879593635
29746152185502371307642255121183693803580388584903
41698116222072977186158236678424689157993532961922
62467957194401269043877107275048102390895523597457
23189706772547915061505504953922979530901129967519
86188088225875314529584099251203829009407770775672
11306739708304724483816533873502340845647058077308
82959174767140363198008187129011875491310547126581
97623331044818386269515456334926366572897563400500
42846280183517070527831839425882145521227251250327
55121603546981200581762165212827652751691296897789
32238195734329339946437501907836945765883352399886
75506164965184775180738168837861091527357929701337
62177842752192623401942399639168044983993173312731
32924185707147349566916674687634660915035914677504
99518671430235219628894890102423325116913619626622
73267460800591547471830798392868535206946944540724
76841822524674417161514036427982273348055556214818
97142617910342598647204516893989422179826088076852
87783646182799346313767754307809363333018982642090
10848802521674670883215120185883543223812876952786
71329612474782464538636993009049310363619763878039
62184073572399794223406235393808339651327408011116
66627891981488087797941876876144230030984490851411
60661826293682836764744779239180335110989069790714
85786944089552990653640447425576083659976645795096
66024396409905389607120198219976047599490197230297
64913982680032973156037120041377903785566085089252
16730939319872750275468906903707539413042652315011
94809377245048795150954100921645863754710598436791
78639167021187492431995700641917969777599028300699
15368713711936614952811305876380278410754449733078
40789923115535562561142322423255033685442488917353
44889911501440648020369068063960672322193204149535
41503128880339536053299340368006977710650566631954
81234880673210146739058568557934581403627822703280
82616570773948327592232845941706525094512325230608
22918802058777319719839450180888072429661980811197
77158542502016545090413245809786882778948721859617
72107838435069186155435662884062257473692284509516
20849603980134001723930671666823555245252804609722
53503534226472524250874054075591789781264330331690
Problem 14
下面的循环数列是由正整数根据以下规则构成的:
n → n/2 (若n是偶数)
n → 3n + 1 (若n是奇数)
若数列从13开始,就生成了如下数列:
13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1
显然以上数列有10个数字,虽然未经证明(著名的Collatz猜想),但我们认为无论由什么数字开始,数列都会在1处结束。故数列一旦产生了1这一项,就认为数列结束。
这次的问题是:根据以上规则,由100万以下的哪个数字开始,可以产生最长的数列?
请注意:产生的数列可能会包含数字超过100万的项。
Problem 15
从一个2×2的方格的左上角开始,共有6条路径可达到右下角(不能后退)

请问,假如把上述方格的规模改成20×20,共有多少条路径呢?
Problem 16
215 = 32768的各位数之和为3 + 2 + 7 + 6 + 8 = 26。
那么21000的各位数之和为……?
Problem 17
如果把1到5写成英语单词的形式:one, two, three, four, five,那么就一共使用了3 + 3 + 5 + 4 + 4 = 19个字母。
若要把1到1000都写成单词的形式,那么总共要使用多少个字母呢?
请注意:不要把空格和连接符都算进去。例如,342(three hundred and forty-two)包含23个字母,115(one hundred and fifteen)含有20个字母。当使用「and」来表达数字时,要遵循英式英语的语法。
Problem 18
从以下的三角形宝塔的最顶点的数开始,一直往下一层的相邻的数移动,所经过的所有数字的和的最大值是23。
3
7 4
2 4 6
8 5 9 3
亦即3 + 7 + 4 + 9 = 23,暂且称之为最大的「宝塔数」吧。
请找出以下「宝塔」的最大宝塔数:
75
95 64
17 47 82
18 35 87 10
20 04 82 47 65
19 01 23 75 03 34
88 02 77 73 07 63 67
99 65 04 28 06 16 70 92
41 41 26 56 83 40 80 70 33
41 48 72 33 47 32 37 16 94 29
53 71 44 65 25 43 91 52 97 51 14
70 11 33 28 77 73 17 78 39 68 17 57
91 71 52 38 17 14 91 43 58 50 27 29 48
63 66 04 68 89 53 67 30 73 16 69 87 40 31
04 62 98 27 23 09 70 98 73 93 38 53 60 04 23
请注意:由于仅有16384条不同的路径,通过尝试扫描所有的路径我们可以找到答案。不过,Problem 67是一个同样的但要求出一个100层的宝塔的最大宝塔数的问题,它不可能用穷举法解决,因此一个巧妙的算法是必需的。
Problem 19
现提供你如下信息,不过你可能希望自己印证一下。
- 1900年1月1日是星期一
- 除了二月外,四月,六月,九月,十一月,都有30天,其他月份都有31天。
- 二月在平年有28天,在闰年有29天。
- 能被4整除的年份是闰年,不过每个世纪年(??00)必须能被400整除才是闰年。
请问,在20世纪中(从1901年1月1日到2000年12月31日)总共有多少个月份的第一日是星期天?
Problem 20
n的阶乘即n! = n × (n - 1) × ... × 3 × 2 × 1。
例如,10! = 10 × 9 × ... × 3 × 2 × 1 = 3628800,并且其结果的每位数的和为3 + 6 + 2 + 8 + 8 + 0 + 0 = 27。
请求出100!的结果的每一位数的和。
Problem 21
设d(n)是小于n的所有能整除n的整数的和。
若d(a) = b,d(b) = a且a ≠ b,那么a和b就是一对相亲数,a和b都被称作是相亲数。
例如,对于220,符合上述条件的整数有1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110,故d(220) = 284。类似地,对于284有1, 2, 4, 71, 142,因此d(284) = 220。
请求出10000以下的全部相亲数的和。
Problem 22
下载这个文档names.txt,这个46KB的文本文档包含超过五千个姓氏,你要先把它们按字母表顺序排列好,然后把姓氏中每个字母在字母表中的索引加总,最后将所有索引的和乘以该姓氏在列表中的索引,就得到该姓氏的分值了。
例如,假定你已经把姓氏列表排好了,找到一个姓氏叫Colin,它的字母索引总和为3 + 15 + 12 + 9 + 14 = 53,已经它是第938个姓氏,于是它的分值就是938 × 53 = 49714。
你知道所有名字的总分值是多少吗?
Problem 23
完全数,就是能表示成其小于自身的所有因数的和的正整数。例如,28可表示成1 + 2 + 4 + 7 + 14 = 28,故28是一个完全数。
一个正整数n,若其小于自身的所有因数的和小于n则n是不足数,若大于则n为充足数。
12是最小的充足数,1 + 2 + 3 + 4 + 6 = 16。能表示成两个充足数的和的最小正整数是24。经数学分析,可知任一超过28123的整数都能写成两个充足数的和。
请求出所有不能表示成两个充足数的和的正整数的和。
Problem 24
一个排列就是物体按一定的顺序摆放。例如,3124是数字1, 2, 3, 4的一种排列。如果所有排列都按照数字顺序或字母顺序排列的话,我们就称之为词法顺列。0, 1, 2的所有词法排列是:
012 021 102 120 201 210
0, 1, 2, 3, 4, 5, 6, 7, 8, 9的第100万个词法排列是……?
Problem 25
Fibonacci数列的定义如下:
Fn = Fn-1 + Fn-2,且F1 = 1, F2 = 1。
于是前12个Fibonacci数就是:
- F1 = 1
- F2 = 1
- F3 = 2
- F4 = 3
- F5 = 5
- F6 = 8
- F7 = 13
- F8 = 21
- F9 = 34
- F10 = 55
- F11 = 89
- F12 = 144
第十二项F12,是第一个达到三位数的Fibonacci数。
第一个达到1000位的Fibonacci数又是多少呢?
Problem 26
分子是1的分数被称作「单分数」。分母从2到10的单分数如下:
- 1/2 = 0.5
- 1/3 = 0.(3)
- 1/4 = 0.25
- 1/5 = 0.2
- 1/6 = 0.1(6)
- 1/7 = 0.(142857)
- 1/8 = 0.125
- 1/9 = 0.(1)
- 1/10 = 0.1
其中,0.1(6)即表示0.166666...,并且它的循环部分只有一个数。由上还能知道1/7的循环部分有6个数。
请找出在1000以内的正整数d,1/d的循环部分最长。
Problem 27
Euler公佈了一个著名的公式:
n² + n + 41
当n = 0 ~ 39时它可以得到40个质数,不过当n = 40时,402 + 40 + 41 = 40(40 + 1) + 41可以被41整除,故当n = 41时得到的不是质数。
通过计算机分析,一个更不可思议的公式诞生了。n² - 79n + 1601能产生80个质数若n = 0 ~ 79。两个系数-79和1601的积是-126479。
现在来看看下面的公式:
n² + an + b且|a| < 1000, |b| < 1000
|n|表示n的绝对值,如|11| = 11|,|-4| = 4。
找出合适的系数a和b,使得当n从0开始递增时,得到最多的连续的质数项,并把a和b的积求出来。
Problem 28
由1开始,按顺时针方顺延伸得到如下5 × 5的螺旋数列:
21 22 23 24 25
20 7 8 9 10
19 6 1 2 11
18 5 4 3 12
17 16 15 14 13
可以算出对角线上所有数字的和为101。
那么用如上构造方法的1001 × 1001的螺旋数列的对角线上的所有数字的和是……?
Problem 29
若2 ≤ a ≤ 5且2 ≤ b ≤ 5,那么ab的所有组合有:
- 22=4, 23=8, 24=16, 25=32
- 32=9, 33=27, 34=81, 35=243
- 42=16, 43=64, 44=256, 45=1024
- 52=25, 53=125, 54=625, 55=3125
将以上数字不重复地从小到大排列,我们得到一个含15项的数列:
4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125
由ab(2 ≤ a ≤ 100且2 ≤ b ≤ 100)产生的如上数列的所有不同的项共有多少个?
Problem 30
有件令人惊奇的事,只有三个四位的正整数等于它们的每位数的4次方的和:
1634 = 14 + 64 + 34 + 44
8208 = 84 + 24 + 04 + 84
9474 = 94 + 44 + 74 + 44
这些数字的和是1634 + 8208 + 9474 = 19316。
你能找出所有能表示成其每位数的5次方的和的所有5位数的和么?
Problem 31
英国的货币单位有英磅(£)和便士(p),流通的货币面值有如下八种:
1p, 2p, 5p, 10p, 20p, 50p, £1 (100p), £2 (200p)
可以这么来凑够两英磅(£2):
1×£1 + 1×50p + 2×20p + 1×5p + 1×2p + 3×1p
请问总共能用多少种方式来凑够两英磅呢?
Problem 32
若一个n位数包含了数字1到n且各仅一次话,就称之为「泛位数的」。例如,5位数15234是一个包含1到5各一次,是泛位数的。
7254是一个不同寻常的积,因为39 × 186 = 7254,其中,被乘数丶乘数和积,是泛位数的,包含了数字1到9。
请找出像上面的7254那样能表示成泛位数的乘积等式的所有积的和。
提示:有些数字能表示成多种乘积的形式,小心不要重复累加。
Problem 33
49/98是个古怪的分数,因为粗心的学生在约分时往往会直接通过去掉数字9得到49/98 = 4/8,不过这结果的确是对的。
把像30/50 = 3/5这样末尾带0的当作是正常的例子吧。
在简化小于1且分子和分母都是两位数的分数时,恰有4个这样不正常的例子。
请求出这四个分数的积的最简化形式的分母。
Problem 34
145是个奇怪的数字,因为1! + 4! + 5! = 1 + 24 + 120 = 145。
请求出能表示成其每位数的阶乘的和的所有数的和。
请注意:由于1! = 1和2! = 2不是和,故它们并不包括在内。
Problem 35
197这个数被称作是环质数,因为1 9 7的三个轮转排列出的数字197, 971, 719都是质数。
100以内总共有13个环质数:2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, 97。
你知道100,0000以内共有多少个环质数吗?
Problem 36
十进制数585=10010010012在十进制和二进制下都是回文数。
请找出所有小于100,0000的在二进制下也是回文数的十进制数的和。
(两位数及以上的以0结尾的数都不是回文数)
Problem 37
数字3797有个奇异的性质,它本身是一个质数,从左到右依次将它的每位数去掉都可以得到一个质数:3797, 797, 97, 7。类似地,从右到左逐个去除每位数,也能得到质数:3797, 379, 37, 3。
像这样的质数总共有11个,请把它们的和求出来。
请注意:2, 3, 5, 7并不包括在内。
Problem 38
将192分别与1, 2, 3相乘:
192 × 1 = 192
192 × 2 = 384
192 × 3 = 576
将各个积连接起来,我们得到一个1到9的泛位数192384576,我们称192384576是192和(1, 2, 3)的「积连接」。
同样地,还可以将9分别与1, 2, 3, 4, 5相乘,得到的积连接是一个1到9的泛位数918273645。
请求出1到9的最大泛位数,并且它是某个整数与(1, 2, ... , n)的积连接(n > 1)。
Problem 39
假设p是某个具有整数边长{a, b, c}的直角三角形的周长,若p = 120,则三边长有三种解:
{20,48,52}, {24,45,51}, {30,40,50}
请求出p ≤ 1000时,使解的数目最多时p的值。
Problem 40
我们可以通过连接相邻的正整数来构造一个不循环小数:
0.123456789101112131415161718192021...
如上,小数部分的第12位数字是1。
若以dn来表示小数部分的第n位数字的话,那么以下算式的结果是多少呢?
d1 × d10 × d100 × d1000 × d10000 × d100000 × d1000000
Problem 41
若一个n位数包含数字1到n且各仅一次,那么就称之为1到n的「泛位数」。例如,2143既是一个1到4的泛位数,又是一个质数。
是质数的最大泛位数是多少呢?
Problem 42
三角数列的第n项是由tn = ½n(n+1)得到的,它的前十项是:
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...
我们把单词中的每个字母和它在字母表中的顺序号一一对应,并把相应的序号相加,就得到了该单词的词彙值。例如,SKY的词彙值是19 + 11 + 25 = 55 = t10。若一个单词的词彙值是三角数的话,就称之为三角单词。
下载words.txt,该文本文档包含近2000个常用英语单词,请统计其中三角单词的数目。
Problem 43
1406357289是一个0到9的泛位数,因为它是由0~9这10个数字按照一定顺序组合而成的。它的子串(其中某些连续数字)有一些奇怪的特性。
令d1为第1位数,d2为第2位数,如此等等。这样,可以看到:
- d2d3d4=406能被2整除
- d3d4d5=063能被3整除
- d4d5d6=635能被5整除
- d5d6d7=357能被7整除
- d6d7d8=572能被11整除
- d7d8d9=728能被13整除
- d8d9d10=289能被17整除
请求出具有上述特性的所有0到9的泛位数的和。
Problem 44
五边形数可由这个函数产生:Pn=n(3n-1)/2。前十个五边形数是:
1, 5, 12, 22, 35, 51, 70, 92, 117, 145
可见,P4 + P7 = 22 + 70 = 92 = P8。不过,它们的差70 - 22 = 48,不是五边形数。
你能否找出两个五边形数,它们的和或差都是五边形数呢?若可以的话,那D = |Pk - Pj|的最小值是多少呢?
Problem 45
三角形数,五边形数,六边形数分别由如下公式生成:
- Triangle Tn=n(n+1)/2 1, 3, 6, 10, 15, ...
- Pentagonal Pn=n(3n-1)/2 1, 5, 12, 22, 35, ...
- Hexagonal Hn=n(2n-1) 1, 6, 15, 28, 45, ...
请找出第二个既是五边形数,又是六边形数的三角形数。已知T285 = P165 = H143 = 40755。
Problem 46
著名的数学家哥德巴赫(Christian Goldbach)曾经提出过一个猜想:每个奇合数都能被表示成一个奇数和某个平方数的两倍的和。例如:
- 9 = 7 + 2×12
- 15 = 7 + 2×22
- 21 = 3 + 2×32
- 25 = 7 + 2×32
- 27 = 19 + 2×22
- 33 = 31 + 2×12
而事实证明这个猜想是错误的。
那么不能用上述形式表达的最小奇合数是多少呢?
Problem 47
第一对各自具有两个不同质因数,并且是相邻整数的数是:
14 = 2 × 7
15 = 3 × 5
首次出现的各自具有三个不同质因数的三个相邻整数是:
644 = 2² × 7 × 23
645 = 3 × 5 × 43
646 = 2 × 17 × 19
你能否找出首批各自具有四个不同质因数的四个相邻整数呢?请指出其中最小的那个数是什么。
Problem 48
已知11 + 22 + 33 + ... + 1010 = 10405071317,
请求出11 + 22 + 33 + ... + 10001000的结果的后10位数。
Problem 49
看这么一个数列:1487, 4817, 8147,其后每一项都是由前一项加上3330得到的。这个数列还有两项特徵:
- 每一项都是质数
- 每一项都是另一项各位数的置换
已知没有任何1位丶2位或3位数能构造出这样的数列,不过还有另外一个如上的4位数递增数列。请找出这个数列,并把那3个数连接成一个12位的数字。
Problem 50
质数41能被表示成6个连续质数的和:
这是在100以下能用最多的连续质数的和表示的质数。
1000以下能表示成最多的连续质数和的质数是953,它能表示成21个连续质数的和。
那100,0000以下能表示成最多连续质数和的质数是……?
Problem 51
通过改变两位数*3的第一位数,可以得到这些质数:13, 23, 43, 53, 73, 83。
把56**3的第三和第四位数用同样的数字替换,得到的10个数字中有7个是质数,这也是第一组具有这个性质的一类数字,这7个质数分别是:56003, 56113, 56333, 56443, 56663, 56773, 56993,故56003是具有如此性质的最小质数。
你能找出这么一个最小质数,将其某几位数用相同的数字替换,包括它自身,能得到8个质数吗?
Problem 52
让我们看看125874和它的两倍251748,它们的各位数的组成都是相同的,只是位置不一样。
请找出一个最小的正整数x,并且2x, 3x, 4x, 5x, 6x都由同样的数字组成。
Problem 53
从5个数字中选出3个,总共有10种方式:
123, 124, 125, 134, 135, 145, 234, 235, 245, 345
在组合数学中,我们将之表示为5C3 = 10。
直到n = 23之前,组合数不会超过一百万:23C10 = 1144066。
问:当1 ≤ n ≤ 100时,有多少个组合数nCr大于100,0000?
Problem 54
扑克游戏中,由五张扑克组成的牌组有着不同的等级,从低到高及其特徵分别是:
- 散牌(High Card):看最大面值的牌。
- 一对(One Pair):有一对相同面值的牌。
- 两对(Two Pairs):有两种不同面值的对子。
- 三条(Three of a Kind):有三张牌面值一样。
- 顺子(Straight):有不同的连续五个面值。
- 同花(Flush):花色都一样。
- 葫芦(Full House):分别有三张面值一样的,另加不同面值的一对。
- 四条(Four of a Kind):有四张相同面值的牌。
- 同花顺(Straight Flush):有花色一样的五个不同的连续面值。
- 同花大顺/一条龙(Royal Flush):有相同花色的10,Jack(骑士),Queen(皇后),King(国王),Ace(黑桃1)。
面值大小的升序排列为:
2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King, Ace.
假如两位玩家都有同类的一手牌,那么相应面值最大者为赢家(如下表,有一对5的比有一对的8小);若相应面值相等,则根据剩下的牌中最大面值来判别输赢(如下表第4行);若剩下的最大面值也一样,则比较次大的面值,如此类推。
以下为参考样例:
| 牌组 | 玩家1 | 玩家2 | 赢家 |
| 1 |
5H 5C 6S 7S KD
一对5
|
2C 3S 8S 8D TD
一对8
|
玩家2 |
| 2 |
5D 8C 9S JS AC
最大是Ace
|
2C 5C 7D 8S QH
最大是Queen
|
玩家1 |
| 3 |
2D 9C AS AH AC
三条Ace
|
3D 6D 7D TD QD
同花
|
玩家2 |
| 4 |
4D 6S 9H QH QC
一对Queen
另有最大牌9 |
3D 6D 7H QD QS
一对Queen
另有最大牌7 |
玩家1 |
| 5 |
2H 2D 4C 4D 4S
葫芦
三条4 |
3C 3D 3S 9S 9D
葫芦
三条3 |
玩家1 |
在文本文档poker.txt中含有1000个回合里两位玩家的牌组,每行有10张牌,前5张是玩家1的,后5张是玩家2的。里面没有不合规则的牌组(故不用检查花色和牌数),但是每张牌都是随意排列的,且没有平局的情况。
请问玩家1赢了多少局?
Problem 55
取质数47,将它逆序相加后,得到47 + 74 = 121,是一个回文数。
并不是取一个质数就能轻易得到回文数的,例如:
349 + 943 = 1292
1292 + 2921 = 4213
4213 + 3124 = 7337
即是说,349要经过3次处理才能得到一个回文数。
虽然还没得到确切证实,但人们认为有些数字,像196,永远都无法通过有限次逆序相加得到一个回文数,这样的数被称为Lychrel数。我们要说明一个数是Lychrel当然就得经过证明。给你1000以下的任何自然数,要么(1)在经过50次及以下的逆序相加后得到一个回文数,要么(2)没有人能不断计算下去得到一个回文数。事实证明,10677是首个发现要经过超过50次逆序相加后才能得到回文数的数字,得到了4668731596684224866951378664(53次逆序相加,28位数)。
令人惊讶的是,有些回文数也是Lychrel数,4994就是那样的数。
问:10000以下的Lychrel数有多少个?
Problem 56
googol数(10100)是一个天文数字:在1的后面接一百个0。100100是个更加难以想像的数字:1的后面接两百个0。不管它们多大,它们各个位上的数字的和都是1。
想想这样的数字,ab,其中a, b < 100,各位数的和最大能是多少?
Problem 57
根号2可以表达成如下无限迭代分数和形式:
√2 = 1 + 1/(2 + 1/(2 + 1/(2 + ... ))) = 1.414213...
展开头四个迭代,可得:
1 + 1/2 = 3/2 = 1.5
1 + 1/(2 + 1/2) = 7/5 = 1.4
1 + 1/(2 + 1/(2 + 1/2)) = 17/12 = 1.41666...
1 + 1/(2 + 1/(2 + 1/(2 + 1/2))) = 41/29 = 1.41379...
再接着的三个迭代的值分别是99/70, 239/169, 577/408,而第8次迭代后的值是1393/985,是首个分子的位数超过分母的位数的迭代。
在前1000次迭代的值中,有多少个值的分子比分母位数多?
Problem 58
由1开始,按逆时针方顺延伸得到如下7 × 7的螺旋数列:
37 36 35 34 33 32 31
38 17 16 15 14 13 30
39 18 5 4 3 12 29
40 19 6 1 2 11 28
41 20 7 8 9 10 27
42 21 22 23 24 25 26
43 44 45 46 47 48 49
有趣的是,其中主对角线的右下部分上的数都是奇平方数。另外,两对角线上质数所占的比例是8/13 ≈ 62%。
如果在上面的数列再延长一圈的话,那么就会得到9 × 9的新数阵。那么,继续延长数列到多少圈,会使两对角线上的质数占对角线数字总个数的百分比小于10%呢?
Problem 59
电脑中的每一个字符都相应着一个特定值,而这个特定值是根据ASCII(美国信息标准交换码)制定的。比如,大写字母A = 65,星号* = 42,小写字母k = 107。
有一个现代的加密方法是,取得一个文本文档,将其内容全都转换成ASCII码,然后用一些固定的特定值(密钥)对每一个ASCII码轮流进行「异或(XOR)」运算,得到密文。用「异或」运算的一个好处是,只要用同样的密钥对每一个加密后的数值再一次按原来的顺序轮流进行异或运算,就能得到原来的ASCII码。看,65 XOR 42 = 107,107 XOR 42 = 65。
想把信息加密得更为牢固的话,可以使密钥的长度和原文一样,密钥的每一个值都是随机取得的,加密者需要将此密钥记录下来以备下次解密之用,否则单靠密文是无法解密的。
可惜的是,这个方法对于多数人来说太不实际了,谁想记住或手动输入这么一大串密钥呢?于是我们得採用比明文(未经加密的信息)短得多的密钥来加密信息。由于密钥变短了,故要循环地利用这个密钥来对每一段与密钥长度相等的个数的ASCII码进行异或运算。密钥不应太短也不应太长,不过只要能轻鬆记住就行了。
这一次,你的任务很简单,文本文档cipher1.txt中的密文(一堆经过加密的ASCII码)是用3个小写字母组成的密钥加密的。明文是一些英语单词,请你将解密后的所有ASCII码的和提交上来。
Problem 60
3, 7, 109, 673是很奇特的一群质数,在其中任取两个任意顺序相连还是能得到一个质数。例如,取7和109相连会有7109和1097两个新的质数。这四个质数的和,792,是具有这种性质的由4个质数组成的集合的最小数值总和。
请找出具由5个质数组成的有如上特殊性质的质数群的数值总和的最小值。
Problem 61
三角形数丶正方形数丶五边形数丶六边形数丶七边形数丶八边形数,都是多边形数,它们都可由以下公式生成:
| 三角形数 | P3,n=n(n+1)/2 | 1, 3, 6, 10, 15, ... |
| 正方形数 | P4,n=n2 | 1, 4, 9, 16, 25, ... |
| 五边形数 | P5,n=n(3n-1)/2 | 1, 5, 12, 22, 35, ... |
| 六边形数 | P6,n=n(2n-1) | 1, 6, 15, 28, 45, ... |
| 七边形数 | P7,n=n(5n-3)/2 | 1, 7, 18, 34, 55, ... |
| 八边形数 | P8,n=n(3n-2) | 1, 8, 21, 40, 65, ... |
有一个由三个四位数构成的数列具有三个有趣的属性:8128, 2882, 8281。
- 这是个循环数列,每个数字的后两位数都是下一个数字的前两位数。
- 每个数的种类都不同:三角形数(P3,127=8128),正方形数(P4,91=8281),五边形数(P5,44=2882),且各自的编号都不同(127, 91, 44)。
- 这是唯一具有以上性质的四位数序列。
现已知有唯一的一个具有如上性质的由六个4位数组成的数列,且数字的种类分别是:三角形数丶正方形数丶五边形数丶六边形数丶七边形数丶八边形数,且编号不同。
Problem 62
立方数41063625 (3453)的每位数经过置换后可以得到另外两个立方数56623104 (3843)和66430125 (4053)。其实,41063625是符合每位数置换后能得到另外两个立方数的最小正整数。
请找出其每位置换后还能得到另外4个立方数的最小立方数。
Problem 63
5位数16807=75是一个5次幂,同样地,9位数134217728=89是一个9次幂。
总共有多少个同时是n次幂的n位正整数呢?
Problem 64
所有正整数的无理数平方根都可以用如下无穷小数的和的形式表示:
| √N = a0 + |
1
|
||
| a1 + | 1 | ||
| a2 + |
1
|
||
| a3 + ... | |||
例如,对于√23有:
| √23 = 4 + √23 - 4 = 4 + |
1
|
= 4 + |
1
|
|
|
1
√23 - 4 |
1 + |
√23 – 3
7 |
||
若继续将其展开,就会得到:
| √23 = 4 + |
1
|
|||
| 1 + |
1 ____
|
|||
| 3 + |
1 ______
|
|||
| 1 + |
1 ________
|
|||
| 8 + ... | ||||
该展开过程有如下的规律:
| a0 = 4, |
1
√23—4
|
= |
√23+4
7 |
= 1 + |
√23—3
7 |
| a1 = 1, |
7
√23—3
|
= |
7(√23+3)
14 |
= 3 + |
√23—3
2 |
| a2 = 3, |
2
√23—3
|
= |
2(√23+3)
14 |
= 1 + |
√23—4
7 |
| a3 = 1, |
7
√23—4
|
= |
7(√23+4)
7 |
= 8 + | √23—4 |
| a4 = 8, |
1
√23—4
|
= |
√23+4
7 |
= 1 + |
√23—3
7 |
| a5 = 1, |
7
√23—3
|
= |
7(√23+3)
14 |
= 3 + |
√23—3
2 |
| a6 = 3, |
2
√23—3
|
= |
2(√23+3)
14 |
= 1 + |
√23—4
7 |
| a7 = 1, |
7
√23—4 |
= |
7(√23+4)
7 |
= 8 + | √23—4 |
可见,这个数列可以循环生成。为了更好地表示每一项,我们把√23的展开式的第4层展开表示成[4;(1,3,1,8)],说明(1,3,1,8)是继续展开后循环出现的部分。
头10个整数的无理数平方根如下:
- √2=[1;(2)],週期=1
- √3=[1;(1,2)],週期=2
- √5=[2;(4)],週期=1
- √6=[2;(2,4)],週期=2
- √7=[2;(1,1,1,4)],週期=4
- √8=[2;(1,4)],週期=2
- √10=[3;(6)],週期=1
- √11=[3;(3,6)],週期=2
- √12= [3;(2,6)],週期=2
- √13=[3;(1,1,1,1,6)],週期=5
说明在小于13的正整数中,只有4个正整数的无理平方根的展开式循环部分週期是1。
在不大于1,0000的正整数中,有多少个正整数的无理平方根的展开式循环部分週期是1?
Problem 65
√2可用无穷个分数的和表示:
| √2 = 1 + |
1
|
|||
| 2 + |
1
|
|||
| 2 + |
1
|
|||
| 2 + |
1
|
|||
| 2 + ... | ||||
我们可将上面的式子简单地写作:√2 = [1;(2)],(2)即表示2要重复出现无数次。又例如说,√23 = [4;(1,3,1,8)]。
这些分数相加的次数越多,其值就越接近要求的数的平方根。现在来看看√2最终会接近(收敛)于怎样的数值吧:
| 1 + |
1
|
= 3/2 |
|
2
|
| 1 + |
1
|
= 7/5 | |
| 2 + |
1
|
||
|
2
|
|||
| 1 + |
1
|
= 17/12 | ||
| 2 + |
1
|
|||
| 2 + |
1
|
|||
|
2
|
||||
| 1 + |
1
|
= 41/29 | |||
| 2 + |
1
|
||||
| 2 + |
1
|
||||
| 2 + |
1
|
||||
|
2
|
|||||
因此头10个接近于√2的数值是:
1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408, 1393/985, 3363/2378, ...
不过数学上有一个著名的常数让人感到无比惊奇:
e = [2; 1,2,1, 1,4,1, 1,6,1 , ... , 1,2k,1, ...]
头10个接近于e的数有:
2, 3, 8/3, 11/4, 19/7, 87/32, 106/39, 193/71, 1264/465, 1457/536, ...
其中第10个数的分子的每位数之和为1+4+5+7=17。
请你找出如上第100个接近e的分数的分子的每位数之和。
Problem 66
看以下的丢番图(Diophantine)方程:
x2 - Dy2 = 1
当D=13时,这个方程的未知数x具有最小值的解为6492 - 13×1802 = 1。
可以肯定的是,当D是平方数时该方程无正整数解。
通过求当D = {2, 3, 5, 6, 7}时未知数x具有最小值的解,可得到:
- 32 - 2×22 = 1
- 22 - 3×12 = 1
- 92 - 5×42 = 1
- 52 - 6×22 = 1
- 82 - 7×32 = 1
因此,当D ≤ 7时,上面要求的未知数x的最大值为9,此时D=5。
若D ≤ 1000,在使未知数x的值最小的解中,当D为多少时,x的值最大?
Problem 67
从以下的三角形宝塔的最顶点的数开始,一直往下一层的相邻的数移动,所经过的所有数字的和的最大值是23。
3
7 4
2 4 6
8 5 9 3
亦即3 + 7 + 4 + 9 = 23,暂且称之为最大的「宝塔数」吧。
请找出这个文档triangle.txt中的宝塔中的最大宝塔数。是不是和18题一样呢?不过这个宝塔有100层!
请注意:这道题比Problem 18难多了,你不可能把所有的路径都走光的,因为它总共包含着299条路径!即使你每秒能处理1012条路径,也要花100亿年才能处理得完。不过有个高效的算法来解决它,嘿嘿。
Problem 68
观察如下奇特的三角环,令六个圆分别被1~6的数字填充,使得每一直线上相连的三个数的和都是9。
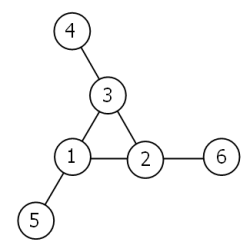
按顺时针方向可将上图中的填充的数字按从外到内的顺序记录下来,则每种填充方式都会有唯一的描述。例如上面的填充方案可表示为4,3,2; 6,2,1; 5,1,3。
总共有8种理想的填充方案,每一直线上相连的数字总和可以是9, 10, 11或12。
| 总和 | 解决方案 |
| 9 | 4,2,3; 5,3,1; 6,1,2 |
| 9 | 4,3,2; 6,2,1; 5,1,3 |
| 10 | 2,3,5; 4,5,1; 6,1,3 |
| 10 | 2,5,3; 6,3,1; 4,1,5 |
| 11 | 1,4,6; 3,6,2; 5,2,4 |
| 11 | 1,6,4; 5,4,2; 3,2,6 |
| 12 | 1,5,6; 2,6,4; 3,4,5 |
| 12 | 1,6,5; 3,5,4; 2,4,6 |
将三组数字连接可得到一个9位数,其中的最大值为432621513。
用1~10十个数字来填充下面的五角环,使得每一直线上相连的数的总和相等,可以有多种解决方案,其中有一些方案的描述可连接成16或17位数,那能连接成的16位数的最大值是……?
Problem 69
欧拉函数φ(n)(有时被称作φ函数)能给既出小于n又与n互质的自然数的个数。如,1, 2, 4, 5, 7, 8都是小于9,但与9互质的数,故φ(9) = 6。
| n | 互质数 | φ(n) | n/φ(n) |
| 2 | 1 | 1 | 2 |
| 3 | 1,2 | 2 | 1.5 |
| 4 | 1,3 | 2 | 2 |
| 5 | 1,2,3,4 | 4 | 1.25 |
| 6 | 1,5 | 2 | 3 |
| 7 | 1,2,3,4,5,6 | 6 | 1.1666... |
| 8 | 1,3,5,7 | 4 | 2 |
| 9 | 1,2,4,5,7,8 | 6 | 1.5 |
| 10 | 1,3,7,9 | 4 | 2.5 |
由上可知在n不大于10的情况下,当n=6时,n/φ(n)达到最小值。
若n ≤ 100,0000,n/φ(n)达到最大值时n的值是多少?
Problem 70
欧拉函数φ(n)(有时被称作φ函数)能给既出小于n又与n互质的自然数的个数。如,1, 2, 4, 5, 7, 8都是小于9,但与9互质的数,故φ(9)=6。
1被认为和任意正整数互质,故φ(1)=1。
有趣的是,φ(87109)=79180,其中,87109是79180每位数的一个置换。
假设1 < n < 107,φ(n)是n的每位数的一个置换,请求出令分数n/φ(n)的值最小的n。
Problem 71
假定有分数n/d,n和d都是正整数。若n<d且GCD(n,d)=1,那么就称它为最简真分数。
分母d不大于8的最简真分数按大小升序排列如下:
1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8
可见紧接着3/7的是2/5。
请你按大小升序列出分母d不大于100,0000的所有最简真分数,并找出紧接着3/7的那个数。
Problem 72
假定有分数n/d,n和d都是正整数。若n<d且GCD(n,d)=1,那么就称它为最简真分数。
分母d不大于8的最简真分数按大小升序排列如下:
1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8
其中总共有21项。
那么分母d不超过100,0000的最简真分数有多少个呢?
Problem 73
假定有分数n/d,n和d都是正整数。若n<d且GCD(n,d)=1,那么就称它为最简真分数。
分母d不大于8的最简真分数按大小升序排列如下:
1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8
可见,1/3和1/2之间有三个分数。
请你按大小升序列出分母d不大于1,2000时的最简真分数,问其中1/3和1/2之间有多少个分数。
Problem 74
145这个数字也有一个奇妙的特徵,它的每位数的阶乘的和又是145:
1! + 4! + 5! = 1 + 24 + 120 = 145
通过这个方式,我们可以发现一个更不为人知的数字169,它产生了最长的最终回到自身的数列。像这样的数列却只有三个:
- 169 → 363601 → 1454 → 169
- 871 → 45361 → 871
- 872 → 45362 → 872
不难证明,每个如上构造的数列最终都不免陷入某种循环。例如:
- 69 → 363600 → 1454 → 169 → 363601 (→ 1454)
- 78 → 45360 → 871 → 45361 (→ 871)
- 540 → 145 (→ 145)
从69开始可最终得到一个5项的不重复数列,而在100,0000以下的最长不重复数列有60项!
请问由100,0000以下的正整数开始构造的这种不重复数列中,有多少个是含60项的?
Problem 75
12是能围成一个整数边长的直角三角形的最小长度,能围成整数边长的直角三角形的长度还有很多:
- 12 : (3,4,5)
- 24 : (6,8,10)
- 30 : (5,12,13)
- 36 : (9,12,15)
- 40 : (8,15,17)
- 48 : (12,16,20)
相反地,像20就不可能是整数边长的直角三角形的周长。而有一些长度就不止是围成一种直角三角形了,例如120的长度能围成三种不同的直角三角形。
120 : (30,40,50), (20,48,52), (24,45,51)
给定整数长度L,当L ≤ 150,0000时总共能围成多少种直角三角形呢?
Problem 76
5可以用6种正整数的和的形式表达:
- 4 + 1
- 3 + 2
- 3 + 1 + 1
- 2 + 2 + 1
- 2 + 1 + 1 + 1
- 1 + 1 + 1 + 1 + 1
问100能用多少种正整数的和的形式表达?
Problem 77
若把10写成质数的和,可有以下5种方式:
- 7 + 3
- 5 + 5
- 5 + 3 + 2
- 3 + 3 + 2 + 2
- 2 + 2 + 2 + 2 + 2
若从小到大研究的话,第一个能用超过5000种方式的质数和表示的自然数是……?
Problem 78
设p(n)是把n个硬币分成几堆的方式的总数。如,5个硬币有7种划分方式,故p(5)=7。
OOOOO |
OOOO O |
OOO OO |
OOO O O |
OO OO O |
OO O O O |
O O O O O |
请找出p(n)能被100,0000整除的最小的n。
Problem 79
网上银行业务的一个常用安全措施是让用户输入某些随机验证码中的某三个字符。例如,验证码是531278,用户被要求输入其中第2丶3丶5个数字,正确输入是317。
这个文本文档,keylog.txt,含有对于同一个验证码的50个成功通过验证的输入。
这些要求的输入的字符都是按顺序给出的,请分析这个文件,并给出最可能短的验证码。
Problem 80
我们都知道,若一个自然数的平方根不是自然数的话,那这个平方根就是一个无理数。无理数的小数部分在十进制下可无限展开却没有循环部分。
2的平方根是1.41421356237309504880...,且它的小数部分的前100位数字的和为475。
请求出前100个自然数(从0或1开始都没关係,因为100 = 102)的所有无理平方根的小数部分前100位数字的和的总和。
Problem 81
在如下5阶方阵中,从左上角向右或向下移动到右下角使得经过的数字的和最小的路径(和为2427)已用红色标记。
|
在文本文档matrix.txt中有一个80×80的方阵,请你求出以如上方式移动所经过的路径的最小和。
Problem 82
提醒:这是Problem 81的升级版。
在如下5阶方阵中,从最左边任一格子向上丶向下或向右移动到最右边任一格子使得经过的数字的和最小的路径(和为994)已用红色标记。
|
在文本文档matrix2.txt中有一个80×80的方阵,请你求出以如上方式移动所经过的路径的最小和。
Problem 83
提醒:这题和Problem 81类似,不过更有意思。
在如下5阶方阵中,从左上角的格子向上丶下丶左丶右四个方向移动到右下角的格子,其间经过的数字(红)的总和为2297。这是能使经过的数字的和最小的路径了。
|
在这个文本文档matrix3.txt中,有一个80阶的方阵,请找出用如上移动方式得到的最佳路径上所有数字的和。
Problem 84
现在你看到的是一个大富翁游戏(Monopoly)的一种标准棋盘:
| GO | A1 | CC1 | A2 | T1 | R1 | B1 | CH1 | B2 | B3 | JAIL |
| H2 | C1 | |||||||||
| T2 | U1 | |||||||||
| H1 | C2 | |||||||||
| CH3 | C3 | |||||||||
| R4 | R2 | |||||||||
| G3 | D1 | |||||||||
| CC3 | CC2 | |||||||||
| G2 | D2 | |||||||||
| G1 | D3 | |||||||||
| G2J | F3 | U2 | F2 | F1 | R3 | E3 | E2 | CH2 | E1 | FP |
玩家从标有GO的格子上开始顺时针移动,并且通过投掷的两个六面骰的面值总和决定移动格子数。若没有任别的规则,那么玩家移动到每个格子上的机率都是2.5%。不过,移动到G2J (Go To Jail,坐牢), CC (community chest,社区福利基金)和CH (chance,赌运气)这些格子上时就会改变这个机率。
除了G2J和来自CC或CH的一张卡片以外,还有别的方式能让玩家去坐牢。若玩家连续投到三次偶数,那么玩家第三次移动则被取消,直接被送到牢狱里去。
游戏一开始时,CC和CH中的卡片都要重新洗牌。当玩家移动到CC或CH上时,他们要从相应的牌堆最顶端拿一张卡片,当完成卡片上的指示后,就把卡片放回相应卡堆的最底下。每个卡堆都有16张卡片,不过由于我们这次的题目的原因,我们只考虑对玩家移动产生影响的卡片,其馀无关的卡片的指示都会被无视,改为让玩家平安地停留在CC或CH格子上。
CC (2/16卡片):
- 回到起点
- 去坐牢
CH (10/16卡片):
- 回到起点Advance to GO
- 去坐牢Go to JAIL
- 去到C1
- 去到E3
- 去到H2
- 去到R1
- 去到下一个R (火车站)
- 去到下一个R
- 去到下一个U (公交站)
- 后退3格
这道题的重点是看到达每个格子的机率是多少,即每次掷骰后能到达特定格子的机率。因此,请注意,每轮掷骰后最终停留的那个格子才是我们要求的到达的格子,故到达G2J的机率必定是0,到达CH的机率最低(因为5/8的卡片都要求再移动)。直接或通过卡片移动到监狱(JAIL)都被看作是一样的,而且不要求抛到偶数才能走出监狱。
从GO开始将格子编号为00到39,我们就能将这些两位数相连得到一个数字来有序地代表一些格子。
经过统计,最常到达的三个格子按顺序分别是:JAIL (6.24%)即10号格子, E3 (3.18%)即24号格子, GO (3.09%)即00号格子。因此可用一个六位数表示:102400。
若不用六面骰(1-6),改用四面骰(1-4),那么最终得到的六位数是……?
Problem 85
在方形的网格上,数数就知道一个3×2的矩形含有18个正方形:
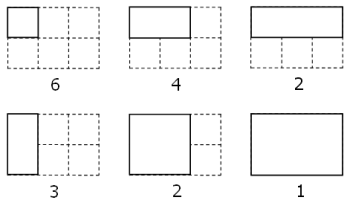
虽然不存在恰好含200,0000个正方形的矩形,不过请你求出所含正方形个数最接近这个数值的矩形的面积。
Problem 86
某蜘蛛S在一长方体的一角上,这个长方体的长宽高分别是6、5、3,在长方体的对角上还有一只苍蝇F。从S至F的最智短「直线」距离是10,路径如图所示:
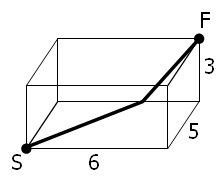
然而,实际上对于任何长方体,像这样的「最短」路径往往可以达到3种,并且最短路径的长不一定是整数。
假设长方体的长宽高的值都是整数且最大不超过整数M,那么当M=100时就有2060种长方体的如上「最短路径」的长是整数,而这个M的值也是使这种长方体的种数超过2000的最小值。当M=99时这样的长方体有1975种。
请找到最小的M,使得这样的长方体种数超过100,0000。
Problem 87
能表示成一个质数的平方加一个质数的立方再加一个质数的四次方的和的最小整数是28。实际上,在50以下只有4个整数能表示成这种形式。
- 28 = 22 + 23 + 24
- 33 = 32 + 23 + 24
- 49 = 52 + 23 + 24
- 47 = 22 + 33 + 24
在5000,0000以下共有多少个整数能用如上形式表示出来呢?
Problem 88
若自然数N能表示成某个元素不少于两个的自然数的有限集合{a1, a2, ... , ak}的元素的「和」与「积」的话,就称这个数为「和·积数」:N = a1 + a2 + ... + ak = a1 × a2 × ... × ak 。
例如,6 = 1 + 2 + 3 = 1 × 2 × 3。
给定有限自然数集合的元素个数为k,则符合这个性质的最小的和·积数在k = 2, 3, 4, 5, 6时分别是:
- k=2: 4 = 2 × 2 = 2 + 2
- k=3: 6 = 1 × 2 × 3 = 1 + 2 + 3
- k=4: 8 = 1 × 1 × 2 × 4 = 1 + 1 + 2 + 4
- k=5: 8 = 1 × 1 × 2 × 2 × 2 = 1 + 1 + 2 + 2 + 2
- k=6: 12 = 1 × 1 × 1 × 1 × 2 × 6 = 1 + 1 + 1 + 1 + 2 + 6
故若2≤k≤6,则所有最小和·积数的和为4+6+8+12 = 30,注意,8只被计算了一次。
已知,当2≤k≤12时,所有最小和·积数为{4, 6, 8, 12, 15, 16},和是61。
那么当2≤k≤12000时的所有最小和·积数的和是……?
Problem 89
罗马记数法为同一个数字提供了许多种记录的方式,然而对于任一个数总是会有「最佳的」记数方式。
举个例子吧,下面都是数字16的罗马记数法:
- IIIIIIIIIIIIIIII
- VIIIIIIIIIII
- VVIIIIII
- XIIIIII
- VVVI
- XVI
上面最下的那个被认为是最佳的记录方式,因为它使用了最少的罗马数字。
这个文本文档roman.txt,内含一千个正确有效的罗马数字,但不保证是用最合适的方法表示的,它们以降序排列(由长到短),并且遵循罗马数字表示规则(如,I只能在V或X前面)。
请问若把每个数字都改写成最佳形式,会节省多少个罗马数字呢?
提示:你可以认为其中不包含超过4个相同的罗马数字。
Problem 90
下面各个骰子的每一面都有不同的点数(0至9),将两个骰子并排,就能构造成一系列的两位数。
如,可能得到平方数64:
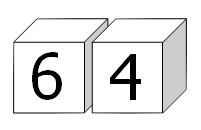
事实上,只要仔细地设定骰子每一面的点数,就能构造出100以下的所有平方数:01, 04, 09, 16, 25, 36, 49, 64, 81。
有一种方法就是,一个骰子各面的点数是{0, 5, 6, 7, 8, 9},另一个骰子的则是{1, 2, 3, 4, 8, 9}。
然而,在这次的问题中,我们允许6和9上下倒转,因此骰子点数的另一种分佈{0, 5, 6, 7, 8, 9}和{1, 2, 3, 4, 6, 7}也可以构造出那9个平方数;否则,不可能构造出09。
我们只关注骰子点数的不同,而不考虑点数的位置:
{1, 2, 3, 4, 5, 6}等同{3, 6, 4, 1, 2, 5}
{1, 2, 3, 4, 5, 6}异于{1, 2, 3, 4, 5, 9}
由于我们允许6和9上下倒转,那两个相异的骰子在构造两位数时都能表示出{1, 2, 3, 4, 5, 6, 9}这些数字。
问:为了构造出100以下的所有平方数,这一对骰子总共有多少种点数分佈方案?
Problem 91
在下面的整数座标系中,有点P(x1, y1)和点Q(x2, y2),它们与原点O(0,0)构成了一个三角形OPQ。
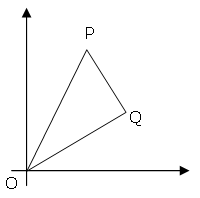
若在每条轴上只能取0-2之间的值,则只能构成14种含有直角的三角形OPQ:

若能在每条轴上取值的范围为0-50,则能构成多少种直角三角形OPQ?
Problem 92
以下数列的构造方法是:前一项的每位数的平方和就是下一项,直到下一项在之前的项中出现过就完成了数列的构造。
44 → 32 → 13 → 10 → 1 → 1
85 → 89 → 145 → 42 → 20 → 4 → 16 → 37 → 58 → 89
显然,上面两个数列假如再用1或89构造下一项的话就会出现循环。然而还有一个令人诧异的事实,就是不管起始项是哪个整数,数列都会以1或89结束。
有多少个以1000,0000以下的正整数为起始项的列数会以89结束呢?
Problem 93
使用集合{1, 2, 3, 4}中每个数字一次,配合四则运算(+, -, *, /)还有括号,可以运算出不同的正整数结果:
- 8 = (4 * (1 + 3)) / 2
- 14 = 4 * (3 + 1 / 2)
- 19 = 4 * (2 + 3) - 1
- 36 = 3 * 4 * (2 + 1)
要注意的是,不能把数字连起来,像12 + 34是不允许的。
使用集合{1, 2, 3, 4}并通过四则运算,可算出31种正整数结果,其中36是最大的,并且1至28都不是首个不能算出的数字(意即29是第一个算不出的)。
请找到这么四个一位数,a < b < c < d,通过四则运算可算得的连续的正整数1到n的数目最多,然后把这四个数组成一串数字abcd。
Problem 94
我们可以很容易证明,等边三角形不可能既有整数边长又有整数面积。然而,近等边三角形5-5-6的面积是12个单位(直角座标系)。
现定义,近等边三角形为有两边相等,而第三边的长度与另外两边的长相差1。
请求出所有周长不超过10,0000,0000且边长和麵积皆为整数的近等边三角形的边长的和。
Problem 95
一个整数的真因数就是除它自身以外的所有因数。如,28的真因数是1, 2, 4, 7, 14,由于它的所有真因数之和为28,因此称28为「完全数」。
有趣的是,220的真因数之和为284,而284的真因数之和为220,我们可称这两个数互为「亲和数」。
不过除此之外还有一个鲜为人知的数列。若是从12496开始,通过前一项的真因数之和构造后一项,可以得到以下含有5项的循环数列:
12496 → 14288 → 15472 → 14536 → 14264 (→ 12496 → ...)
这样的循环数列就是「亲和数列」。
请找到这么一个亲和数列,它的每一项都不超过100,0000,并且项数最多。问:这个数列的最小项是……?
Problem 96
数独(SuDoku,日语即「摆放数字」的意思)是一个有趣的益智项目。虽然不知它源自何处,不过我们不得不讚歎欧拉(Leonhard Euler),因为他曾发明过一个类似的更有难度的迷题——拉丁方阵(Latin Squares)。而原来的数独游戏是这样的:分别用1~9九个数字不重复地将9×9的大方阵中3×3的小方阵中的空格或零替代,并使大方阵的每一行和每一列上的数字都不重复。如下是一个典型的初始方阵,及最终的解决方案:
|
|
一个精心构造的数独方阵只会有一个解法,而且能通过逻辑来解决,或许要进行一些假设来确定一下摆放的位置(关于这个有多种的观点)。推理的複杂性体现了游戏的难度,上面这个例子就被认为是「简单」的,因为人们能通过直接的推论来解决它。
这个文本文档sudoku.txt里包含了50个不同难度的数独方阵,且每个都只有唯一的解。
这次的挑战是:解出这50个数独方阵,并将所有方阵的左上角三个数字组成的三位数的和求出来。如,上面给出的方阵的左上角三个数字组成的三位数是483。
Problem 97
第一个超过一百万位的质数是人们在1999年发现的,它被称作梅森质数,因为它具有如此的形式:26972593-1。确切地说,它有209,8960位数。后来人们发现了更多的含更多位数的梅森质数,它们都能表示为2p-1。
然而,在2004年,人们又发现了一个巨大的非梅森质数28433×27830457+1,它有235,7207位数。
请找出这个质数的最后10位数。
Problem 98
将单词CARE的每个字母分别用1, 2, 9, 6来替换,可得到一个平方数:1296 = 362。奇特的是,用同样的方式来替换,CARE的变形词RACE也能变成一个平方数:9216 = 962。于是称CARE和RACE是一对平方数变换词。另外请注意,不允许有前导的0,各种字母替换成的数字也不能相同。
在文本文档words.txt里有将近2000个常见英语单词,请找出所有的平方数变换词对,看其中最大的平方数是多少。(回文词不能算是自身的变形词,如「A」)
请注意:所有变形词必须被包含有那个文档中。
Problem 99
比较两个指数形式的数如211和37是没有难度的,因为随便一个计算器都会告诉你211 = 2048 < 37 = 2187。
但是偏偏有一些数字的比较让一般的计算器也难以判断,如632382518061 > 519432525806,这两个数都超过了300万位。
在文本文档base_exp.txt中含有一千行数字,每行有一个底数和一个指数,代表一个数的指数形式,请判断哪一行的数字最大。
Problem 100
某箱子里有21个彩色圆盘,其中15个是蓝色的,6个是红色的。若随机抽取两个圆盘,那么取到两个蓝色圆盘的概率是(15/21)×(14/20) = 1/2。
另外还有一个箱子,随机取得两个蓝色圆盘的概率也是50%,箱子中的圆盘有85个是蓝色的,有35个是红色的。
请你找到第一个内含超过1012 = 1,000,000,000,000个圆盘的箱子,随机取到两个蓝色圆盘的概率也是50%,请问这个箱子中有多少个蓝色圆盘?
Problem 101
若只提供某个数列的前k项,我们是无法断定下一项是什么的,因为能生成那样开头的数列的多项式公式能有无穷种。
举个例子吧,看看立方数的序列,它们是由以下方程生成的:
un = n3: 1, 8, 27, 64, 125, 216, ...
假如我们只知道这个数列的头两项,根据「简单原则」,我们很可能会先假设各项之间具有线性关係,并且下一项是15(等差数列,差是7)。就算还知道了第三项,按照简单原则,我们还是很可能会弄出二次方程关係来(译注:设an = an2+bn+c,下面的多项式优化类同,就是求解a, b, c, ...等系数,得到多项式公式)。
假设OP(k, n)是最优化后的多项式公式生成的立方数数列的第n项,必须保证的是,OP(k, n)对于n ≤ k是有效的。往往,第一个不符项(first incorrect term, FIT)就是OP(k, k+1),这时我们称这个公式为不良优化公式(bad OP, BOP)。
先从最简单的开始,若只知道数列的第一项,那么最简单的方式就是假设数列都是常数项,即,当n ≥ 2时,OP(1, n) = u1。
于是通过简单原则,我们最终得到立方数数列的最优化多项式生成公式OP:
| OP(1, n) = 1 | 1, 1, 1, 1, ... |
| OP(2, n) = 7n-6 | 1, 8, 15, ... |
| OP(3, n) = 6n2-11n+6 | 1, 8, 27, 58, ... |
| OP(4, n) = n3 | 1, 8, 27, 64, 125, ... |
显然,对于k ≥ 4,BOP不存在(译注:有n3了,还用得着更高次方吗?)。
由上可知,所有BOP(已用红色标记)的FIT的和为1 + 15 + 58 = 74。
请考虑以下数列,公式已经出,请找到优化过程中所有BOP的FIT和。
un = 1 - n + n2 - n3 + n4 - n5 + n6 - n7 + n8 - n9 + n10
Problem 102
在平面上随机取3个点,其座标的取范围都是-1000 ≤ x, y ≤ 1000,以这三点为顶点构造三角形。
看看以两个三角形(顶点):
A(-340,495), B(-153,-910), C(835,-947)
X(-175,41), Y(-421,-714), Z(574,-645)
其中,只有三角形ABC内含有原点。
在文本文档triangles.txt中含有1000个随机三角形(的三个顶点座标),请检测出其中有多少个三角形含有原点(0, 0)。
Problem 103
让我们用S(A)来表示某元素个数为n的集合A中数字的总和。某集合的任意两个不相交的非空子集B和C若符合以下两个条件,则称它为「异和集」:
- S(B) ≠ S(C)
- 若B的元素比C的多,则S(B) > S(C)
若S(A)相关的n值达到最小,则称A为最优异和集。以S(A)为参照,头5个最优异和集如下:
- n = 1: {1}
- n = 2: {1, 2}
- n = 3: {2, 3, 4}
- n = 4: {3, 5, 6, 7}
- n = 5: {6, 9, 11, 12, 13}
我们可以发现,似乎某个最优集合A = {a1, a2, ... , an}的下一个最优集合是这样的:B = {b, a1+b, a2+b, ... ,an+b},其中,b是前一个集合的靠近中间的元素。
通过运用这个假设的规则,我们可推测n = 6时的最优异和集是A = {11, 17, 20, 22, 23, 24},且S(A) = 117。然而,这并不是最优的,我们只是运用这个简单的算法得到一个接近优化的结果。实际上,此时的最优异和集该是A = {11, 18, 19, 20, 22, 25},且S(A) = 115,设定其对应的数字串是排列后的元素的连接111819202225。
请找到当n = 7时的最优异和集对应的数字串。
Problem 104
Fibonacci数列的递归定义如下:
Fn = Fn-1 + Fn-2,且F1 = 1, F2 = 1。
已知F541有113位数,而且它是第一个最后9位数是1至9的泛位数的项。另外,F2749有575位数,它是首个开头9位数是1至9的泛位数的项。
假设Fk是第一个具有这样性质的Fibonacci数:前10位数和后10位数都是1至9的泛位数。请求出k的值。
Problem 105
让我们用S(A)来表示某元素个数为n的集合A中数字的总和。某集合的任意两个不相交的非空子集B和C若符合以下两个条件,则称它为「异和集」:
- S(B) ≠ S(C)
- 若B的元素比C的多,则S(B) > S(C)
例如,{81, 88, 75, 42, 87, 84, 86, 65}不是「异和集」,因为65 + 87 + 88 = 75 + 81 + 84;而{157, 150, 164, 119, 79, 159, 161, 139, 158}的所有非空子集都符合上述两个条件,它的S(A) = 1286。
在文本文档sets.txt中含有100个数集,每个含有7至12个元素。(头两个集合就是上例中的)请找出所有「异和集」 A1, A2, ..., Ak,且求出S(A1) + S(A2) + ... + S(Ak)。
Problem 106
让我们用S(A)来表示某元素个数为n的集合A中数字的总和。某集合的任意两个不相交的非空子集B和C若符合以下两个条件,则称它为「异和集」:
- S(B) ≠ S(C)
- 若B的元素比C的多,则S(B) > S(C)
在此问题中,我们假定所有集合中的元素都按升序排列了,并且它们都满足上述第二个条件。
令人惊奇的是,在n = 4的集合的25对非空子集中,只有1对需要测试他们是否满足第一个条件。同样地,当n = 7时,966对子集中只有70对需要测试第一个条件。
当n = 12时,在261625对非空子集中,有多少对必须进行第一个条件的检测?
Problem 107
以下网络含7个接点,12条边,总负荷为243。
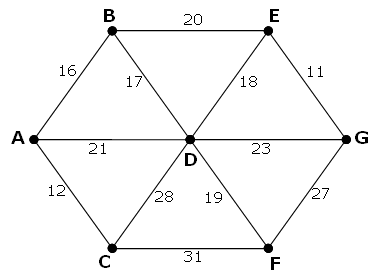
其矩阵描述形式如下:
| A | B | C | D | E | F | G | |
| A | - | 16 | 12 | 21 | - | - | - |
| B | 16 | - | - | 17 | 20 | - | - |
| C | 12 | - | - | 28 | - | 31 | - |
| D | 21 | 17 | 28 | - | 18 | 19 | 23 |
| E | - | 20 | - | 18 | - | - | 11 |
| F | - | - | 31 | 19 | - | - | 27 |
| G | - | - | - | 23 | 11 | 27 | - |
不过,我们可以去掉某些边,而网络依旧是连通的。以下就是该网络达到最小负荷时的连通情况,总负荷为93,相对原先的减少了243 - 93 = 150。
在文本文档network.txt中,给出了一个具有40个接点的网络的矩阵形式,请在保持网格连通的情况下,找到改良后能最节省成本的网络的总负荷。
Problem 108
有如下方程,x, y, n都是正整数:
|
1
x |
+ |
1
y |
= |
1
n |
若n = 4则有三种解:
|
1
5 |
+ |
1
20 |
= |
1
4 |
|
1
6 |
+ |
1
12 |
= |
1
4 |
|
1
8 |
+ |
1
8 |
= |
1
4 |
能令这个方程有超过1000种不同解的n的最小值是……?
注意:这是problem 110的简单版本,不过,强烈建议你先解决目前这个问题。
Problem 109
在一场飞镖游戏中,每个玩家能投掷三个飞镖,靶子被等分为20个区域,它们被标号为1~20。

得分将由飞镖所在靶子上的区域号码决定。在红绿环以外的不计分,在黑白环上的记一倍(×1)分数,而在红绿环上的,由外到内分别能得到两倍(×3)和三倍(×3)的分数。
靶心分两部分,掷中外圈得25分,内圈得50分。
这种游戏有很多的玩法,其中最受欢迎的一种是:每人一开始有301分或501分,首先把分值降到0的人就胜出。不过,一般还会加上一个「加倍终局」限制,即,玩家必须在最后一镖投中一个「加倍分数」(包括红绿环和靶心),否则投到的其他能让分值降到0或以下的得分都不计。(译注:貌似走题了……)
当玩家结束游戏时,它们的评分记录最高可为170:20×3 20×3 25(两20分的内红绿环和一个外靶心25).
得到6分的方式有11种:
| 3×2 | ||
| 1×2 | 2×2 | |
| 2×1 | 2×2 | |
| 2×2 | 1×2 | |
| 4×1 | 1×2 | |
| 1×1 | 1×1 | 2×2 |
| 1×1 | 1×3 | 1×2 |
| 1×1 | 3×1 | 1×2 |
| 1×2 | 1×2 | 1×2 |
| 1×2 | 2×1 | 1×2 |
| 2×1 | 2×1 | 1×2 |
注意,1×2 2×2与2×2 1×2不同,因为它们是不同区域分数的加倍,不过,1×1 1×3 1×2是认为与1×3 1×1 1×2相同的。
另外,我们不必考虑投不中的情况。譬如说,3×2等同于0 3×2和0 0 3×2。
已知所有的得分方式加起来总共有42336这么多。
那么得分低于100的方式有多少种呢?
Problem 110
有如下方程,x, y, n皆为正整数:
|
1
x |
+ |
1
y |
= |
1
n |
当n = 1260时,有113个不同的解,这时的n也是让该方程的解超过100个的最小值。
若该方程的解有超过400,0000种,则n的最小值是……?
提醒:这题比problem 108难得多,无法暴力求解,故需要一点小窍门。
Problem 111
假设4位的质数包含重复的数字,那么它的每位数不能都是一样的:1111能被11整除,2222能被22整除,如此等等。而所有含三个重复数字的4位质数有9个:
1117, 1151, 1171, 1181, 1511, 1811, 2111, 4111, 8111
现在我们用M(n, d)来表示n位的质数中重复数字d最多有多少个,用N(n, d)来表示重复数字有M(n, d)个的 n位质数的个数,再用S(n, d)表示这些质数的和。
因此,M(4, 1) = 3是4位的质数中1最多能重复3个(译注:即是说唯一的1111不是质数,只能取3次重复),且N(4, 1) = 9,S(4, 1) = 22275。当d = 0时,虽然M(4, 0) = 2,不过N(4, 0) = 13。
就这样,我们可以得到关于4位质数的一些信息:
| 数字d | M(4, d) | N(4, d) | S(4, d) |
| 0 | 2 | 13 | 67061 |
| 1 | 3 | 9 | 22275 |
| 2 | 3 | 1 | 2221 |
| 3 | 3 | 12 | 46214 |
| 4 | 3 | 2 | 8888 |
| 5 | 3 | 1 | 5557 |
| 6 | 3 | 1 | 6661 |
| 7 | 3 | 9 | 57863 |
| 8 | 3 | 1 | 8887 |
| 9 | 3 | 7 | 48073 |
当0 ≤ d ≤ 9时,所有S(4, d)的和是273700。
请求出所有S(10, d)的和。
Problem 112
若一个数的每位数由左到右逐渐增大,那就称之为「上升数」,如134468。同理,还有「下降数」,如66420。
此外,再把既不上上升数又不是下降数的正整数称为「弹性数」,如155349。
显然,在100以下不存在任何弹性数。不过在1000以内有525个弹性数。经统计,第一个使弹性数的比例达到或超过50%的上限是538。
当上限越来越大时,弹性数的比重就越来越大。上限为21780时弹性数的比例为90%。
请找出弹性数的比例为99%(准确值)时的最小上限。
Problem 113
若一个数的每位数由左到右逐渐增大,那就称之为「上升数」,如134468。同理,还有「下降数」,如66420。
此外,再把既不上上升数又不是下降数的正整数称为「弹性数」,如155349。
当上限n增大时,不超过n的弹性数也增多,而在100,0000以下有12951个非弹性数,在1010以下有277032个非弹性数。
问:在googol数(10100)以下有多少个非弹性数?
Problem 114
将一排7个砖块(长度为1)中的几块用长度不小于3的红色砖块替换,任意两个红色砖块间至少间隔一个黑色砖块(否则视为一块红砖),那么则有以下17种替换方案:
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||
若是一排有50个黑色方块,又有多少种替换方式呢?
Problem 115
提醒:这题比problem 114难一点。
一排n个黑色砖块(长度为1)中的某些或全部被长度至少为m的红色砖块替换了,且两块红色砖块之间至少隔着一块黑色砖块。
设函数F(m, n)表示上述砖块的替换方案总数。
例如,F(3, 29) = 673135,F(3, 30) = 1089155。
上述例子说明,当m = 3时,n = 30是能使替换方案总数超过100,0000的最小数字。
同样地,当m = 10时,F(10, 56) = 880711且F(10, 57) = 1148904,因此n = 57是使替换方案超过100,0000的最小数字。
问:当m = 50时,使F(50, n)超过100,0000的n至少是多少?
Problem 116
一排五个黑色砖块(长度为1)中的某些砖块被不同颜色的砖块替换了,有红色的(长度为2),有绿色的(长度为3),有蓝色的(长度为4)。
若只用红色砖块替换,那么就有以下7种替换方式:
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
若只用绿色砖块,则有3种:
|
|
|
|
||||||||||||||||
若只用蓝色砖块,则有2种:
|
|
|
||||||||||
这样,若只用一种颜色的砖块来替换,总共就有7 + 3 + 2 = 12种替换方式。
若是一排上有50个黑色砖块,那么只用一种颜色的砖块(红、绿、蓝)来替换,总共有多少种替换方案呢?
提示:这题是problem 117的简单版本。
Problem 117
用不同颜色的砖块将一排五个黑色砖块(长度为1)中的某些砖块替换,用的砖换有红色的(长度为2),有绿色的(长度为3),有蓝色的(长度为4)。总共有15种替换方式:
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
若是一开始一排上有50个黑色砖块,那么总共有多少种替换方式呢?
提醒:这题是problem 116的困难版本。
Problem 118
仅用1至9的数字各一次构成整数,可以组成多种集合。有些集合很有趣,如{2,5,47,89,631},其中所有的数字都是质数。
问所有这些集合中仅包括质数的集合有多少个?
Problem 119
512有个有趣的性质,它是它的每位数之和的幂:5 + 1 + 2 = 8且83 = 512。像这样的数字还有614656 = 284。
设an是第n个具有这种性质的不少于两位数的正整数,已知a2 = 512且a10 = 614656,请求出a30。
Problem 120
设r是(a-1)n + (a+1)n被a2除了之后的馀数。
例如,当a = 7和n = 3时,r = 42,63 + 83 = 728 ≡ 42 mod 49。当a = 7时,r随着n的大小变化会有最大值rmax= 42。
请把当3 ≤ a ≤ 1000时所有情况下r的最大值的和∑rmax求出来。
Problem 121
某袋子里有一个红色圆片和一个蓝色圆片,在一次赌博中,玩家从中随机摸出一个,并把颜色记下来,接着把圆片放回去,并且再加多一个红色圆片。下一回合又重新随机摸出一个。
每玩一次游戏收费1英磅,若是游戏结束时所记下的蓝色比红色多的话就算赢。
假如只玩四个回合,那么胜出的机率是11/120,相应地,庄家能提供的奖金至多是10英磅(1÷11/120≈10.9,向下取整则为10),以防亏损过多。还要注意的是,交易中的钱都是整数英磅的,并且奖金中实际包含了1英磅的费用,故玩家实际赢得的最高奖金是9英磅。
若是玩15个回合,奖金至多该是多少呢?
Problem 122
一般来说我们计算n15需要进行14次乘法运算:
n × n × ... × n = n15
不过,通过一个「二次」方式,你只须乘6次:
- n × n = n2
- n2 × n2 = n4
- n4 × n4 = n8
- n8 × n4 = n12
- n12 × n2 = n14
- n14 × n = n15
然而你可能要5次就够了:
- n × n = n2
- n2 × n = n3
- n3 × n3 = n6
- n6 × n6 = n12
- n12 × n3 = n15
设m(k)是计算nk所需的最少相乘次数,那么m(15) = 5。
令1 ≤ k ≤ 200,请求出所有m(k)的和。
Problem 123
设pn是第n个质数:2, 3, 5, 7, 11, ...令r为(pn-1)n + (pn+1)n除以pn2的馀数。
譬如说,当n = 3, p3 = 5时,43 + 63 = 280 ≡ 5 (mod 25)。
能使馀数r超过109的最小质数是p7037,此时n = 7037。
那么能使馀数r超过1010的最小的n是……?
Problem 124
设rad(n)是n的所有质因数的积,如,504 = 23 × 32 × 7,因此rad(504) = 2 × 3 × 7 = 42。
若我们求出rad(n)在1 ≤ n ≤ 10时的所有情况,且将结果按rad(n)的大小排列,若rad(n)相等则再比较n的大小来排序,可得:
|
未排序
|
已排序
|
|||
|
n
|
rad(n)
|
n
|
rad(n)
|
k
|
|
1
|
1
|
1
|
1
|
1
|
|
2
|
2
|
2
|
2
|
2
|
|
3
|
3
|
4
|
2
|
3
|
|
4
|
2
|
8
|
2
|
4
|
|
5
|
5
|
3
|
3
|
5
|
|
6
|
6
|
9
|
3
|
6
|
|
7
|
7
|
5
|
5
|
7
|
|
8
|
2
|
6
|
6
|
8
|
|
9
|
3
|
7
|
7
|
9
|
|
10
|
10
|
10
|
10
|
10
|
令E(k)是排序后的第k项,会有E(4) = 8,E(6) = 9。
若考虑1 ≤ n ≤ 100000的所有情况,那么E(10000)是……?
Problem 125
595是个有趣的回文数,它能够被表示成五个连续平方数的和:62 + 72 + 82 + 92 + 102 + 112 + 122。
1000以下总共有11个这样的回文楼,且他们的和为4164。注意,1 = 02 + 12由于0不是正整数,因而没有被包括在内。
108以下又有多少个这样的回文数呢?请你把它们的和求出来。
Problem 126
要遮住一个3×2×1的长方体的每一面至少需要22个立方体:
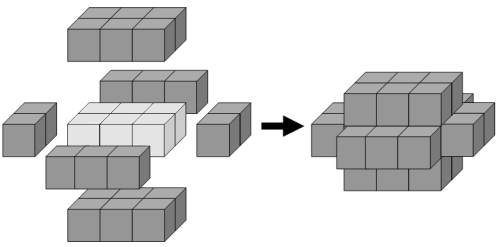
若是要给上面得到的新立体再加上第二层把每一面都遮住,则需要46个立方体;如此,加第三层覆盖则需要78个立方体,加第四层则需要118个。
碰巧的是,5×1×1的长方体的第一层覆盖也需要22个立方体;类似的还有,5×3×1、7×2×1、11×1×1的长方体的第一层覆盖都需要46个立方体。
不妨用C(n)表示在某一层覆盖中需要n个立方体的长方体的个数,则C(22) = 2, C(46) = 4, C(78) = 5, C(118) = 8。
已知,当154是符合C(n) = 10的最小n值。
请找到符合C(n) = 1000的最小n值。
Problem 127
设rad(n)是n的所有质因数的积,如,504 = 23 × 32 × 7,因此rad(504) = 2 × 3 × 7 = 42。
满足以下所有条件的正整数三元组(a, b, c)被称为「abc组」:
- GCD(a, b) = GCD(a, c) = GCD(b, c) = 1(译注:a, b, c两两互质)
- a < b
- a + b = c
- rad(abc) < c
如,(5, 27, 32)是一个abc组,因为:
- GCD(5, 27) = GCD(5, 32) = GCD(27, 32) = 1
- 5 < 27
- 5 + 27 = 32
- rad(4320) = 30 < 32
看来abc组是很少的,当c < 1000时只有31个,且Σc = 12523。
请求出当c < 12,0000的所有abc组的Σc。
Problem 128
从1号六边形的「12点方向」开始,将2到7号六边形按逆时针环绕它,新的环也是以同样的方式添加的,8到19,20到37,38到61,等等。下图展示了三个环。
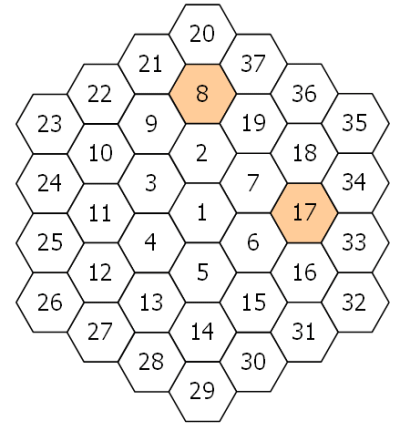
通过检查n号方块与相邻数字的差,我们定义PD(n)为这些差之中质数的个数。
如,按顺时针方向看8号周围的数字,它们与8分别相差12, 29, 11, 6, 1, 13,因此PD(8) = 3。
同样地,7与其相邻数字之差分别为1, 17, 16, 1, 11, 10,于是PD(17) = 2。
可验证,(译注:无论有多少圈)PD(n)的最大值是3。
若将所有PD(n) = 3的数字按升序(译注:从小到大)排列出来,那么第10个数会是271。
请找到这个数列中的第2000个数。
Problem 129
我们把一个完全由1构成的整数称为循环单位,并用R(k)来表示位数为k的循环单位。如,R(6) = 111111。
假设有正整数n,且n与10互质,可证明对于n总存在一个值k,R(k)能被n整除。设A(n)是满足此条件的最小的k值。如,A(7) = 6,A(41) = 5。
n使A(n)超过10的最小值是17。
n使A(n)超过100,0000的最小值是多少呢?
Problem 130
我们把一个完全由1构成的整数称为循环单位,并用R(k)来表示k位数的循环单位。如,R(6) = 111111。
假设有正整数n,且n与10互质,可证明对于n总存在一个值k,R(k)能被n整除。设A(n)是满足此条件的最小的k值。如,A(7) = 6,A(41) = 5。
又可证明,对于大于5的质数p,p - 1可被A(p)整除。如,当p = 41时,A(41) = 5且40可被5整除。
然而,少数的合数也有上面的性质,具有此性质的最小5个合数依次是91, 259, 451, 481, 703。
请求出最小的25个合数n的和,n与10互质,且n - 1能被A(n)整除。
Problem 131
对于某些质数p,存在一个正整数n,使n3 + n2p为一完全立方数。
如,当p = 19时,83 + 82×19 = 123 。
神奇的是,任一个这样的质数,其n的值都是唯一的,不会与其他质数的重复。已知在100以下只有4个这样的质数。
请问在100,0000以下,有多少个这样的质数?
Problem 132
我们把一个完全由1构成的整数称为循环单位,并用R(k)来表示位数是k的循环单位。
如,R(10) = 1111111111 = 11×41×271×9091,其质因数的总和为9414。
请求出R(109)最小的前40个质因数的和。(译注:还是质因数分解的前40个最小项的和呢?)
Problem 133
我们把一个完全由1构成的整数称为循环单位,并用R(k)来表示k位数的循环单位。如,R(6) = 111111。
现在来看看这种形式的循环单位:R(10n)。
虽然R(10), R(100), R(1000)都不能被17整除,不过R(10000)可以。然而,不存在能被19整除的R(10n)。已知,能整除R(10n)的100以下的质数只有11, 17, 41, 73。
请求出10,0000以下不可能是R(10n)的因数的所有质数的总和。
Problem 134
请看这两个相邻的质数p1 = 19和p2 = 23,1219是以p1结尾并能被p2整除的最小正整数。
已知,除了p1 = 3和p2 = 5是一个例外,对于其余的所有相邻质数p2 > p1,总存在正整数n,其为既由p1结尾,又能被p2整除的数字,令S为n的最小值。
请求出5 ≤ p1 ≤ 100,0000范围以内的所有S的总和。
Problem 135
有正整数x, y, z,是某个方程中的三个变量。正整数n在方程x2 - y2 - z2 = n有解时的最小值是27,此时方程的解有两种:
342 - 272 - 202 = 122 - 92 - 62 = 27
当方程有10种解时,n的最小值是1155。
当方程有10种解时,n小于100,0000的情况有多少个?
Problem 136
有方程x2 - y2 - z2 = n,x, y, z, n都是正整数,当n = 20时,此方程只有一个解:
132 - 102 - 72 = 20
已知在100以下能使该方程有唯一解的n的值只有25个。
那么,在5000,0000以下使方程有唯一解的n值有多少个?
Problem 137
定义某无穷多项式的值为AF(x) = xF1 + x2F2 + x3F3 + ...,其中,Fk是Fibonacci数列:1, 1, 2, 3, 5, 8, ...中的第k项,Fk = Fk-1 + Fk-2,且F1 = 1, F2 = 1。
在这次的问题中,我们只须关心AF(x)是正整数的情况。
| 如AF(1/2) | = | (1/2).1 + (1/2)2.1 + (1/2)3.2 + (1/2)4.3 + (1/2)5.5 + ... |
| = | 1/2 + 1/4 + 2/8 + 3/16 + 5/32 + ... | |
| = | 2 |
AF(x)的前五个自然数值及对应的x的值如下表所示:
| x | AF(x) |
| √2-1 | 1 |
| 1/2 | 2 |
| (√13-2)/3 | 3 |
| (√89-5)/8 | 4 |
| (√34-3)/5 | 5 |
我们应该称x为有理数的AF(x)为「金子」,因为它们越来越稀少了,第10块「金子」已经是7404,9690了。
请找到第15块「金子」。
Problem 138
现有这么一个等腰三角形,它的底边长b = 16,两腰长L = 17。

根据毕达哥拉斯定理,可算出该三角形的高h = √(172 - 82) = 15,它仅比底边长小1。
若b = 272且L = 305,则h = 273,仅比底边长大1。这是拥有这类性质的第二小的等腰三角形,即h = b ± 1。
请找到这类等腰三角形中最小的那十二个,求出它们的腰长L的总和。
Problem 139
用(a, b, c)来代表一个直角三角形的三边长,a, b, c都是整数。由样的四个直角三角形可以用来构成一个边长为c的正方形。
举个例子,四个三角形(3, 4, 5)可构造出一个5×5的正方形,其中有一个1×1的洞,可见,5×5的正方形能用25个1×1的方块拼成。

而用(5, 12, 13)构成的13×13的正方形中间会有个7×7的洞,13×13的方形不能用7×7的方块拼成。
若直角三角形的周长小于100,0000,那么有多少种三角形,以其构成的大正方形能被中间的小正方形空洞拼成?
Problem 140
有无限多项式公式AG(x) = xG1 + x2G2 + x3G3 + ...,其中Gk是这个二次递归函数生成数列的第k项:Gk = Gk![]() 1 + Gk
1 + Gk![]() 2, G1 = 1且G2 = 4,即生成数列1, 4, 5, 9, 14, 23, ...
2, G1 = 1且G2 = 4,即生成数列1, 4, 5, 9, 14, 23, ...
在本次的问题中,我们只需要考虑AG(x)为正整数时的变量x。
AG(x)为前五个正整数时对应的x如下表:
| x | AG(x) |
| (√5-1)/4 | 1 |
| 2/5 | 2 |
| (√22-2)/6 | 3 |
| (√137-5)/14 | 4 |
| 1/2 | 5 |
假如x为有理数我们就称AG(x)为「金子」,因为x为有理数的情况会随着AG(x)的增大变得越来越少。如,第20个金子是211345365。
请求出前30个金子的和。
Problem 141
某些正整数n,被d除,得商和余数分别为q和r,并且d, q, r是构成了等比数列的三个正整数,不过它们在数列中的顺序并不重要。
例如,58除6商9余4,可见,4, 6, 9构成了等比数列(公比是3/2)。
这样的数字n被称为「渐进数」。
有些渐进数,像9和10404 = 1022,恰好还是完全平方数。
已知10,0000以下的所有渐进完全平方数的和为124657。
请求出1012以下所有渐进完全平方数的和。
Problem 142
有三个正整数x, y, z,x > y > z > 0且x + y, x - y, x + z, x - z, y + z, y - z都是完全平方数,那么x + y + z的最小值是……?
Problem 143
设三角形ABC的每个内角都不大于120度,X为该三角形中的任意点,设XA = p, XB = q, XC = r。
Fermat要考考Torricelli,让他找出当p + q + r最小时,X的位置。
Torricelli证明了,在三角形ABC的每一边上构造等边三角形AOB, BNC, AMC,这三个三角形的外接圆会相交于一点T,且T点在三角形内。另外他还证明,T点就是使p + q + r最小的X的位置,这个点被称为Torricelli/Fermat点。然而更甚的是,当p + q + r达到最小值时,AN = BM = CO = p + q + r,并且AN, BM, CO也交于T点。
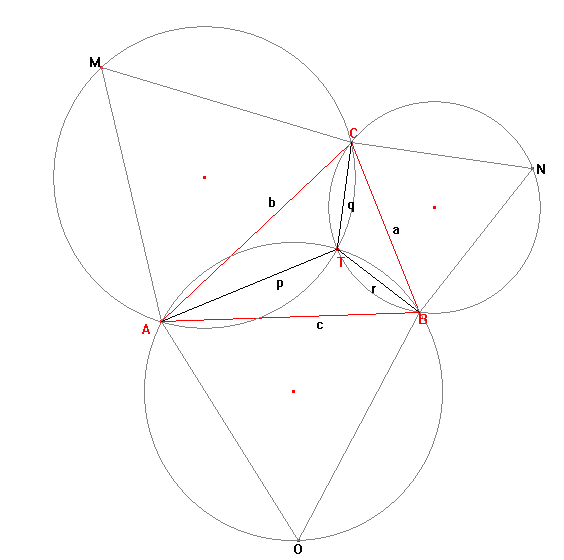
若p + q + r达到最小值,且a, b, c, p, q, r都是正整数的话,我们就称三角形ABC是Torricelli三角。例如,a = 399, b = 455, c = 511时,该三角形就是Torricelli三角,此时p + q + r = 784。
请求出所有不同的Torricelli三角的p + q + r的和,且p + q + r ≤ 120000。
Problem 144
在激光物理学中,有个反光镜系统被称作「白卵(white cell)」,它是用来滞延激光束的。激光束进入白卵中后会在内壁的镜面上不断进行反射,最终从入口处返回。
这次我们采用的白卵是一个椭圆,将其表示为方程为4x2 + y2 = 100。
椭圆顶部的-0.01 ≤ x ≤ +0.01的区域没有了,为的是让激光束进出白卵。
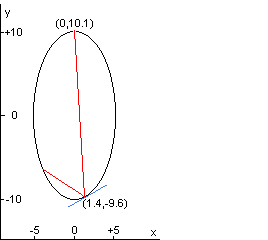
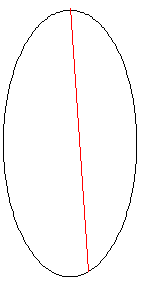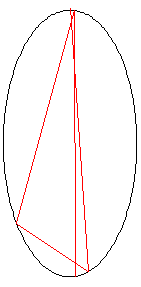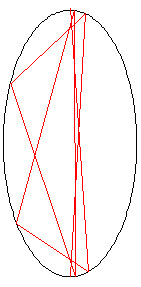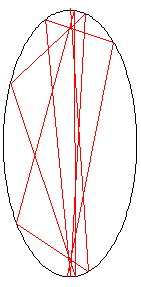
现在某激光束从点(0.0,10.1)进入白卵,首次反射是位于点(1.4,-9.6)。
每当这激光束射中椭圆形白卵的内壁时,都会遵循反射定律,即「入射角与反射角相等」,也即是说,入射光线和反射光线与入射点上的法线之间形成的角度的大小是一样的。
在左图中,红线指示了头两个激光束在白卵内壁上的接触点,蓝线表示的是在第一个入射点上外切于椭圆的直线。
已知,过椭圆上任一点(x, y)的切线的斜率m都为-4x/y,且法线过入射点垂直于该点上的切线。
右图展示的是该激光束的前10次反射。
请问:该激光束在离开白卵之前总共反射了多少次?
Problem 145
某些正整数n具有这样的性质:n与n的倒置之和的每位数都是奇数。如,36 + 63 = 99,409 + 904 = 1313。于是我们把这种数字称为「可逆数」。但n或n的倒置不可出现前置的0(如012, 210)。
1000以下有120个可逆数。
那么10,0000,0000(十亿)以下有多少个可逆数呢?
Problem 146
能使n2+1, n2+3, n2+7, n2+9, n2+13, n2+27是连续的质数的最小正整数n是10,而在100,0000以下符合条件的所有正整数n的总和为1242490。
那么在1,5000,0000以下符合条件的所有正整数n的和是……?
Problem 147
在一个3x2的画有交叉线的格子中,总共可以构造37个矩形:

有5种格子的尺寸小于3x2,在垂直或水平上我们都认为有区别,即1x1, 2x1, 3x1, 1x2, 2x2。若它们都是画有交叉线的,那么我们能在其中构造的矩形数如下所示:
- 1x1:1
- 2x1:4
- 3x1:8
- 1x2:4
- 2x2:18
将以上的数据应用到上面所有37种3x2格子中,总共有72(译注:37+35)种矩形能嵌进3×2和更小的格子中。
那么总共能将多少种矩形嵌进47x43和更小的格子中呢?
Problem 148
可以轻易地证明,Pascal三角的前7层中没有一个数能被7整除:
| 1 | ||||||||||||
| 1 | 1 | |||||||||||
| 1 | 2 | 1 | ||||||||||
| 1 | 3 | 3 | 1 | |||||||||
| 1 | 4 | 6 | 4 | 1 | ||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 |
然而,若检查前100层的5050个数字,其中只有2361个是不能被7整除的。
请找出Pascal三角的前109层中不能被7整除的数字的总个数。
Problem 149
看看下面的表格,易见在同一条直线(水平线、竖直线、对角线)上的任意个相邻数字之和最大可为16 = 8 + 7 + 1。
| -2 | 5 | 3 | 2 |
| 9 | -6 | 5 | 1 |
| 3 | 2 | 7 | 3 |
| -1 | 8 | -4 | 8 |
现在,让我们在更大的表格上寻找这样的和。
首先,要生成400,0000个伪随机数,生成伪随机数的公式叫做「滞后Fibonacci数生成器」:
当1 ≤ k ≤ 55时,Sk = [100003 - 200003k + 300007k3] mod 1000000 - 500000
当56 ≤ k ≤ 4000000时,Sk = [Sk-24 + Sk-55 + 1000000] mod 1000000 - 500000
如,S10 = -393027,S100 = 86613。
接着,Sk的值被填充到一张2000×2000的表格中,前2000个Sk值在第一行,下2000个则在第二行,如此等等。
最后,就是要找到在同一方直线上任意个相邻数字之和的最大值了。
Problem 150
我们想在一个正整数和负整数的三角形数列中,找到一个子三角形数列,使其中的数字之和最小。
在下面的例子中,容易证明,标记出来的三角形数列满足了我们的条件,其中的数字之和为-42。
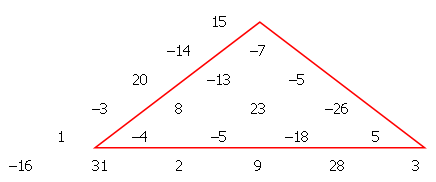
为了构造一个具有1000行的三角形数列,我们在±219的范围内产生了500500个伪随机数sk,伪随机数产生器(线性同余)如下:
t := 0
for k = 1 up to k = 500500:
t := (615949*t + 797807) mod 220
sk := t-219
于是:s1 = 273519, s2 = -153582, s3 = 450905等。
这样,我们就能利用这些伪随机数构造三角形数列了:
s2 s3
s7 s8 s9 s10
...
子三角形数列可从任一项开始,最少一行(只有一项)。(第二行有2项,第三行有3项,如此等等)
请找到其中的一个子三角形数列,使其中的数字之和最小。
Problem 151
某家打印店每周都要进行16批工作,每批工作都需要一张A5大小的特殊抗染色纸。
第天早上,工头都会打开一个装有一张特殊A1纸的包裹,把A1纸取出来。
他会把这张纸裁剪成两半,于是就得到了两张A2纸;接着他又把其中一张A2纸剪成两半,得到两张A3纸;如此下去,直到得到一张A5纸,然后拿去完成每周的第一批工作。
其余没有用到的纸,都会被放回那个包裹里。
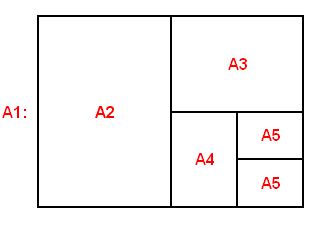
对于接下来的每一批工作,他都会从包裹中随机抽出一张纸。若纸不是A5大小的,他就会不断以「剪成两半」的方式得到所需的一张A5纸,最后剩下的纸还是放回到包裹中。
现除去首次和末次的两批工作,请求出每周这个工头在拿纸张时只找到一张纸的次数的平均值。
答案要精确到小数点后6位。
Problem 152
有几种方法可以将1/2表示为一组不同的数字的平方的倒数之和。
例如,可用{2,3,4,5,7,12,15,20,28,35}:
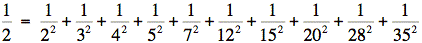
事实上,仅用2到45的部分数字就有三种方法做到这点了,除上面所示的一组数字之外还有{2,3,4,6,7,9,10,20,28,35,36,45}和{2,3,4,6,7,9,12,15,28,30,35,36,45}。
那么用2到80的部分数字,将1/2表示为这些不同数字的平方的倒数之和的方式有多少种呢?
Problem 153
众所周知,方程x2=-1没有实数解。
不过,假如我们认识了虚数i的话,上述方程就有两个解:x=i和x=-i。
这样,像复杂一点的方程(x-3)2=-4也会有两个复数解:x=3+2i和x=3-2i。x=3+2i和x=3-2i互为共轭数。
形如a+bi的数被称作「复数」,而a+bi和a-bi互为共轭数。
若复数a+bi中的a和b皆为整数,则该复数为「高斯整数」。
一般的整数也被称为高斯整数(b=0)。为了将它们与b ≠ 0的高斯整数区分开来,我们又称它们为「实整数」。
某高斯整数能「整除」实整数n,当且仅当除得的结果也是高斯整数。例如,将5除以1+2i,化简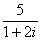 的方法如下:
的方法如下:
将分子与分母同乘以1+2i的共轭数:1-2i。
结果为 。
。
故1+2i能整除5。
而1+i不能整除5,因为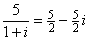 。
。
另外,若高斯整数(a+bi)能整除实整数n,那么它的共轭数(a-bi)也能整除n。
已知,有6个实数部分为正数的高斯整数能整除5:{1, 1 + 2i, 1 - 2i, 2 + i, 2 - i, 5}。
下表展示了前五个正实整数的所有能将其整除的实数部分为正数的高斯整数:
| n | 能整除n的实数部分为正数的高斯整数 | 这些高斯整数的和s(n) |
| 1 | 1 | 1 |
| 2 | 1, 1+i, 1-i, 2 | 5 |
| 3 | 1, 3 | 4 |
| 4 | 1, 1+i, 1-i, 2, 2+2i, 2-2i,4 | 13 |
| 5 | 1, 1+2i, 1-2i, 2+i, 2-i, 5 | 12 |
于是,根据上表我们得到: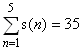 。
。
已知,若1 ≤ n ≤ 105,∑s(n)=17924657155。
问:若1 ≤ n ≤ 108,∑s(n)是……?
Problem 154
某三角金字塔是由圆球构成的,在上面的每一个圆球之下都压着三个圆球。
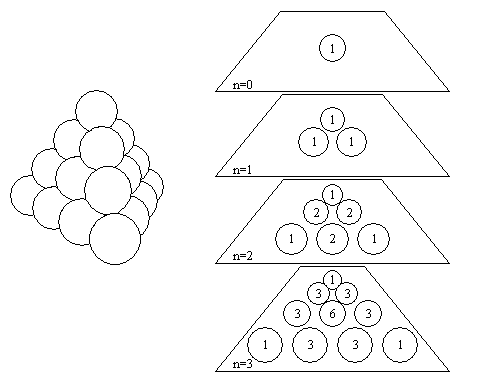
接着,我们要计算从顶端到其余位置的路径条数:
一条路径从顶端的圆球开始,可不断地通向其下三个圆球中的任意一个。
因此,通往某个位置的路径条数是到那个位置之上所有球的路径条数之和。(其上有多少个球取决于其位置)
这个问题的结果被称为Pascal金字塔,其第n层的数字(译注:即从顶端到达某个球的路径条数)是三项式(x + y + z)n的展开式的所有系数。
问:(x + y + z)200000的展开式的所有系数中,有多少个是1012的倍数?
Problem 155
某个电路用的电容器都是专门订造的,种类只有一个,且电容都为C。
我们可将这些电容器串联或并联组合出新的元件,新的元件又可以继续联合起来构造更大的元件,最终得到一个更为复杂的电路。
因此我们能以上述的方式使用n个电容器,构造出一系列不同电容的元件。比如说,若n=3,每个电容器的电容C=60μF,可构造以下7种不同电容的元件:
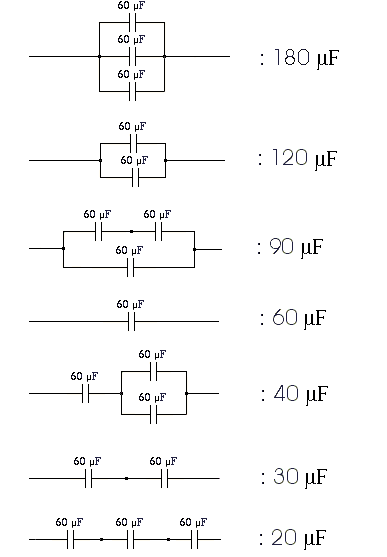
设D(n)为使用n个相同的电容器所能构造的不同电容的元件的种数,则:D(1)=1, D(2)=3, D(3)=7 ...
请求出D(18)的值。
提示:若两个电容器的电容分别为C1, C2,那么当它们并联时的总电容为CT = C1 + C2 +...,当串联时则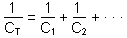 。
。
Problem 156
从0开始,像这样把十进制的自然数写下来:
0 1 2 3 4 5 6 7 8 9 10 11 12....
现在看位数d=1,每次写下一个数字n之后,我们都会统计位数1已经出现过的次数f(n,1)。前几个f(n,1)如下:
| n | f(n,1) |
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 1 |
| 4 | 1 |
| 5 | 1 |
| 6 | 1 |
| 7 | 1 |
| 8 | 1 |
| 9 | 1 |
| 10 | 2 |
| 11 | 4 |
| 12 | 5 |
注意了,f(n,1)永远不会等于3。
因此f(n,1)=n的头两个解分别是n=0和n=1,下一个解是n=199981。
以同样的方式,我们设f(n,d)为位数d在写下数字n后总共被写下的次数。
已知,对于任意位数d ≠ 0,0是f(n,d)=n的第一个解。
设s(d)为f(n,d)=n所有的解的和。现在你得知,s(1)=22786974071。
请求出∑s(d),1 ≤ d ≤ 9。
Problem 157
现有丢番图(Diophantine)方程1/a+1/b= p/10n,a, b, p, n皆为正整数,且a ≤ b。
若n = 1,则该方程总共有20个解,如下表所示:
| 1/1+1/1=20/10 | 1/1+1/2=15/10 | 1/1+1/5=12/10 | 1/1+1/10=11/10 | 1/2+1/2=10/10 |
| 1/2+1/5=7/10 | 1/2+1/10=6/10 | 1/3+1/6=5/10 | 1/3+1/15=4/10 | 1/4+1/4=5/10 |
| 1/4+1/20=3/10 | 1/5+1/5=4/10 | 1/5+1/10=3/10 | 1/6+1/30=2/10 | 1/10+1/10=2/10 |
| 1/11+1/110=1/10 | 1/12+1/60=1/10 | 1/14+1/35=1/10 | 1/15+1/30=1/10 | 1/20+1/20=1/10 |
那么,在1 ≤ n ≤ 9的范围内总共有多少个解呢?
Problem 158
从英语字母表中挑出三个不同的字母,可以构造一串字符,如'abc', 'hat', 'zyx'。
看看这串字符,'abc'中有两个是按字母表顺序挨在左边相邻的字符上的,'hat'中则只有一个,而'zyx'中一个也没有。
在所有长度为三的字符串中,有10400个是只有一个字符按字母表顺序挨在左边相邻字符上的。
现在来看由不多于26个不同的英文字母组成的字符串。
设p(n)为长度为n的字符串中只有一个字符按字母表顺序挨在左边相邻字符上的字符串的个数。
那么p(n)的最大值是……?
Problem 159
一个合数的因式分解有很多种,如,不包含因数1,24的因式分解有如下7种:
- 24 = 2x2x2x3
- 24 = 2x3x4
- 24 = 2x2x6
- 24 = 4x6
- 24 = 3x8
- 24 = 2x12
- 24 = 24
请回想以前介绍过的「数字根」,在十进制下,是由将数字的所有位上的数加起来,得到的和若不小于10则重复这个过程,直到得到一个小于10的数字,那就是数字根。如,467的数字根是8。
这回,我们定义「数字根和」为数字的因式分解中所有数字的数字根的和。
在这个问题中,我们只讨论不含因数1的因式分解。
如下为24的各个数字根和:
| 因式分解 | 数字根和 |
|---|---|
|
2x2x2x3
|
9
|
|
2x3x4
|
9
|
|
2x2x6
|
10
|
|
4x6
|
10
|
|
3x8
|
11
|
|
2x12
|
5
|
|
24
|
6
|
可见,24的最大数字根和为11。
设mdrs(n)为n的最大数字根和,则mdrs(24)=11。
请在1 < n < 100,0000的范围内,求Σmdrs(n)。
Problem 160
给定任意正整数N,设f(N)为N!除末尾连续的0之前的5位数。
例如,
- 9! = 362880,f(9)=36288
- 10! = 3628800,f(10)=36288
- 20! = 2432902008176640000,f(20)=17664
请求出f(1,0000,0000,0000)。
Problem 161
「三格骨牌」是由三个同样的正方形边对边组成的图形(译注:多格骨牌的一种),它有两种基本的形式:
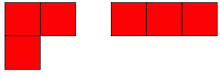
若是把不同的方向也考虑进去,就有六种基本形式:
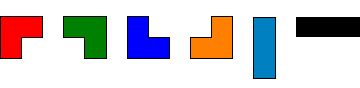
对于任意n×m的区域,若n×m能被3整除,那么它就能被三格骨牌铺满。
若是将经过反射或旋转的填充方式看作是不同的方案(译注:除非和之前完全相同),那么要用三格骨牌铺满2×9的区域总共有41种方式:
若是用三格骨牌铺满9×12的区域,则共有多少种方式呢?
Problem 162
十六进制计数系统使用16种数字:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
十六进制数AF转换成十进制数即10×16+15=175。
在三位的十六进制数10A, 1A0, A10, A01中,都含有数字0,1, A。
像书写十进制数一样,十六进制数也不加前置的0。
有多少个最多十六位的十六进制数包括数字0,1, A都至少一个呢?
请用十六进制数提交你的答案。
(A,B,C,D,E,F用要大写,没有表示十六进制数的前缀或后缀。如,应该像是1A3F,而不是像1a3f或0x1a3f甚至$1A3F或#1A3F还有0000001A3F这样的。)
Problem 163
请先看一下面图尺码为1号的等边三角形,其内部还有从各顶点出发的中线。
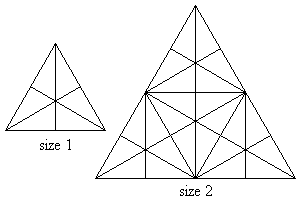
这个等边三角形总共包含16个不同形状、不同大小、不同朝向或不同位置的三角形。现在用这个尺码为1号的三角形为基本单元,构造更大的三角形。如右边那个2号大小的三角形,其中总共包含104个三角形。
可见,2号大小的三角形由四个单元组成,3号大小的则要9个单元,尺码为n号的要用n2个单元构造。
设T(n)为n号大小的三角形总共含有的三角形个数,那么:
- T(1) = 16
- T(2) = 104
请求出T(36)。
Problem 164
请求出具有这个性质的20位的整数的个数(不含前导的0):任意连续三个位上的数的和都不超过9。
Problem 165
一条线段由它的两个端点唯一地确定。
在平面几何中,两条线段的关系有以三种情况:没有交点,有且只有一个交点,有无数个交点。
此外,当两条线段有且只有一个交点时,或许这个交点是其中一条或两条线段的端点。若交点不是任一条线段的端点,那么它就是两条线段的内交点。
若交点T是线段L1和L2的唯一交点,且是内交点,我们则称T点是线段L1和L2的真交点。
现在看以下三条线段:
- L1:(27, 44) 到 (12, 32)
- L2:(46, 53) 到 (17, 62)
- L3:(46, 70) 到 (22, 40)
可证明,线段L2和L3有一个真交点,而线段L3的一个端点(22,40)在L1上,故该点不可能是真交点,另外,L1和L2没有交点。因此,在这三条线段之间,我们只找到一个真交点。
现在我们继续在5000条线段之间找,为此,我们用一个叫做「嗙啷嗙啷唰」的伪随机数生成器产生了20000个数字:
s0 = 290797
sn+1 = sn×sn mod 50515093
tn = sn mod 500
要生成每一条线段,只需要取连续的四项tn作为端点坐标即可。第一条线段是:(t1, t2) 到 (t3, t4)
这个伪随机数生成器生成的前4项为:27, 144, 12, 232。因此第一条线段是从(27,144)到(12,232)。
那么在这5000条线段间总共有多少个真交点呢?
Problem 166
某4×4的表格被0到9的数字填充了:
6 3 3 0
5 0 4 3
0 7 1 4
1 2 4 5
可见,它的每一行或每一列上数字的和都是12,连两条对角线上数字的和都分别是12。
问:用0到9的数字来填充这个4×4的表格,总共有多少种方式能使得每一行、每一列和每条对角线上的数字之和皆相等?
Problem 167
对于任意两个正整数a和b,有Ulam数列U(a,b),U(a,b)1 = a, U(a,b)2 = b,当k > 2时,U(a,b)k为只能写成其前面唯一的两项的和,且大于U(a,b)(k-1)的最小数字。
例如,数列U(1,2)的前几项是:
1, 2, 3 = 1 + 2, 4 = 1 + 3, 6 = 2 + 4, 8 = 2 + 6, 11 = 3 + 8
5不属于这个数列,因为5 = 1 + 4 = 2 + 3,有两种表示为前面两项的和方法。同样地,7 = 1 + 6 = 3 + 4也不在这个数列中。
请求出在2 ≤ n ≤ 10的范围中,∑U(2,2n+1)k的值,其中k = 1011。
Problem 168
只要将142857的每位数旋转右移,就能得到数字714285。
可证明,714285=5 × 142857。
这样就揭示了142857的一个性质:它可以整除它自身经过旋转右移后的数字。
请求出正整数10 < n < 10100中具有这种性质的所有数字的和的最右边5位数。
Problem 169
设f(0)=1,且设f(n)为正整数n能用2的整数幂之和表示的方式的种数,每个整数幂最多只能重复一次。
如,f(10)=5,因为总共有5种方式来表示10:
- 1 + 1 + 8
- 1 + 1 + 4 + 4
- 1 + 1 + 2 + 2 + 4
- 2 + 4 + 4
- 2 + 8
那么,f(1025)的值是……?
Problem 170
将数字6分别乘以1273和9854:
- 6 × 1273 = 7638
- 6 × 9854 = 59124
接着把乘积首尾连接起来,可得到一个1到9的泛位数763859124,我们称763859124为6和(1273, 9854)的「积连接」。另外还请注意了,数字6, 1273, 9854连起来也是一个1到9的泛位数612739854。
这些做法也能应用到0到9的泛位数上。
请找到这么一个0到9的泛位数,其为某个整数和其它两个或更多的整数的「积连接」,且这些整数的连接也是一个0到9的泛位数。
Problem 171
对于正整数n,设f(n)为它的(十进制下)每位数的平方的和,如:
- f(3) = 32 = 9
- f(25) = 22 + 52 = 4 + 25 = 29
- f(442) = 42 + 42 + 22 = 16 + 16 + 4 = 36
请在0 < n < 1020的范围中,求出所有满足f(n)是完全平方数的n的和,并提交计算结果的最后9位数。
Problem 172
有多少个18位整数(没有前置的0)没有一位数出现超过3次?
Problem 173
假定要做出这么一个方形铁板,它中间有个方形的洞,这块铁板是上下对称和左右对称的。比如,用32块方形铁片,我们可以做出以下两种方形铁板:

若是最多能用100块铁片,那么我们可以做出51种不同的方形铁板。
若是最多能用100,0000块铁片,则可做出多少种?
Problem 174
假定要做出这么一个方形铁板,它中间有个方形的洞,这块铁板是上下对称和左右对称的。
若用8块方形铁片,则只能做出一种:3×3的铁板中有一个1×1的洞。而用32块铁板可做出如下两种:

设t是使用的方形铁片数,以能做的铁板种数将t = 8或32的情况分类为用L(1)和L(2)。
再设N(n)是t ≤ 1000000时属于L(n)一类的t的情况总数,如,N(15) = 832。
那么当1 ≤ n ≤ 10时,所有N(n)的总和是……?
Problem 175
设f(0)=1,且设f(n)为正整数n能用2的整数幂之和表示的方式的种数,每个整数幂最多只能重复一次。
例如,f(10)=5,因为10有如下5种表示方式:
10 = 8+2 = 8+1+1 = 4+4+2 = 4+2+2+1+1 = 4+4+1+1
可证明,对于每一个分数p/q(p>0, q>0),至少存在一个正整数n,使得f(n)/f(n-1)=p/q。
如,使得f(n)/f(n-1)=13/17的最小的n是241。另外,241的二进制值为11110001,从这个数的最高位看到最低位,有4个1、3个0和1个1,我们称「4,3,1」为241的二进制缩写。
请求出满足f(n)/f(n-1)=123456789/987654321的最小n的二进制缩写。
注意,缩写中的数字要用逗号分隔,不留空白。
Problem 176
有四个直角三角形,其三边长各自为(9,12,15), (12,16,20), (5,12,13), (12,35,37),它们都有一条较短的边(直角边)的边长为12。除此之外,没有任何纯整数边长的直角三角形再具有边长为12的直角边。
请找到最小的整数边长,其为47547种不同的纯整数边长的直角三角形的某直角边的边长。
Problem 177
假设有突四边形ABCD,并连上了对角线AC和BD,这样四边形的每个顶点上都有被对角线分出的两个角,总共有八个角。

譬如说,在顶点A上,分别有两个角∠CAD和∠CAB。
若这样的四边形的这八个角度都是整数,则称它为「整数角四边形」。其中一种整数角四边形就是正方形,那八个角都是45°。还有整数角四边形如∠DAC = 20°, ∠BAC = 60°, ∠ABD = 50°, ∠CBD = 30°, ∠BCA = 40°, ∠DCA = 30°, ∠CDB = 80°, ∠ADB = 50°。
请问:总共有多少种不相似的整数角四边形?
注意:在计算中,整数角度容差为10-9,即是说,角度值的小数部分在此范围内的角都被当作是整数角。
Problem 178
让我们好好来地看一下45656这个数字:它的相邻两个数字之差皆为1,这样的数被称之为「阶梯数」。
而含有0到9所有数字至少一次的数就叫「全数数」。
不知在1040以下有多少个整数既为阶梯数,又为全数数呢?
Problem 179
令1 < n < 107,且n和n + 1有同样多的正因数,那么这样的n总共有多少个?例如,14的正因数有1, 2, 7, 14,15的正因数有1, 3, 5, 15。
Problem 180
有这么三个关于任意整数n的函数:
f1,n(x,y,z) = xn+1 + yn+1 - zn+1
f2,n(x,y,z) = (xy + yz + zx)*(xn-1 + yn-1 - zn-1)
f3,n(x,y,z) = xyz*(xn-2 + yn-2 - zn-2)
将这三个函数组合成一个新的函数:
fn(x,y,z) = f1,n(x,y,z) + f2,n(x,y,z) - f3,n(x,y,z)
我们称(x,y,z)为k阶黄金三元组,若x, y, z 都是具有如此形式的有理数:a / b,且0 < a < b ≤ k ,并且存在一个整数n,使得fn(x,y,z) = 0。
设s(x,y,z) = x + y + z,再设t = u / v 为所有35阶黄金三元组(x,y,z)的所有不同s(x,y,z)的和,所有的s(x,y,z),还有t都必须是最简形式。
请求出u + v。
Problem 181
现在有3个黑色的物体B和1个白色的物体W,它们能够用7种方式堆放起来,像这样:
| (BBBW) | (B,BBW) | (B,B,BW) | (B,B,B,W) | (B,BB,W) | (BBB,W) | (BB,BW) |
那么假如有60个黑色物体B和40个白色物体W,能有多少种方式来堆放它们呢?
Problem 182
著名的RSA加密算法是基于如下算法实现的:
- 生成两个不同的素数p和q
- 令n = pq, φ = (p-1)(q-1)
- 找到一个整数e,1 < e < φ,使gcd(e,φ) = 1
- 每個基本信息单元的数字编码在[0, n-1]之间
- 每份包含大量信息的明文都將被转化为一堆数字编码([0, n-1])
- 要加密文本,对于其中的每个信息单元m,就要算出对应的数字编码c = me mod n,这便是加密
- 而要破解密文,就必须找出d,ed mod φ = 1,接着对于每个数字编码c,计算出明文信息m = cd mod n
另外,满足me mod n = m的e和m有很多。
我们称信息单元m为未加密信息,若me mod n = m。
在选择恰当的e时,得避免造成过多信息未经加密。
如,设p=19, q=37,
接着n = 19×37 = 703, φ = 18×36 = 648,
若选定e = 181,那么即使gcd(181, 648) = 1,信息单元m(0 ≤ m ≤ n-1)都无法加密,因为me mod n = m。
因此对于任意有效的e来说都存在相应的未加密信息单元。
而我们的目的就是要将未加密信息单元的数量限制到最小。
现在令p = 1009, q = 3643,请求出所有这样的e的和,1 < e < φ(1009,3643)且gcd(e, φ) = 1,使得造成未加密信息单元数量最少。
Problem 183
N是一正整数,把N等分成k份,r = N/k,这样,N = r + r + ... + r。
令P = r × r × ... × r = rk。
譬如说,若11被等分为5份,11 = 2.2 + 2.2 + 2.2 + 2.2 + 2.2,则P = 2.25 = 51.53632。
现设M(N) = Pmax,即对于N,P能达到的最大值。
那么,当把N = 11平分为4份时,就有Pmax = (11/4)4,即M(11) = 14641/256 = 57.19140625,它是一个不循环小数。
不过,若N = 8,则平分为3份时有M(8) = 512/27,这是一个无限循环小数。
现再设D(N) = N若M(N)是个无限循环小数,且D(N) = -N若M(N)是个不循环小数。
如,当5 ≤ N ≤ 100时,ΣD(N) = 2438。(译注:Σ是求和符号)
问:当5 ≤ N ≤ 10000时,ΣD(N)为多少?
Problem 184
假设Ir为圆心在直角坐标坐标系原点上的半径为r的圆中,所有坐标为整数的点(x,y)的集合,亦即有x2 + y2 ![]() r2。
r2。
假设圆的半径为2,那么I2含有点(0,0), (1,0), (1,1), (0,1), (-1,1), (-1,0), (-1,-1), (0,-1), (1,-1),以这些点为顶点,且包围圆心的三角形总共有8个。其中两个三角形如图所示,其它的只要将这两个三角形旋转几次就能得到:
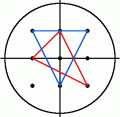
假设半径为3,那么这样的三角形就有360个了。若半径为5,则有10600个。
若半径为105,那么这样的三角形又有多少个呢?
Problem 185
一会将要介绍的游戏「猜数字(Number Mind)」是一个出名的叫做「珠玑妙算(Master Mind)」的游戏的变体。
你不用猜珠子,而是要猜一系列按顺序排列的数字。每猜一次,你都会被告知有几个位置上的数字猜对了,因而,若答案是1234,你猜2036的话,就会告诉你有一个位置猜中了。不过,(译注:和Master Mind不同的是)你不会知道有多少个猜到的数字放错了位置。
游戏如下,猜5个数字:
- 90342 -对了2个
- 70794 -对了0个
- 39458 -对了2个
- 34109 -对了1个
- 51545 -对了2个
- 12531 -对了1个
而正确答案是39542,根据上面的过程,这个答案是唯一的。
现在,请根据下面的猜测过程……
- 5616185650518293 -对了2个
- 3847439647293047 -对了1个
- 5855462940810587 -对了3个
- 9742855507068353 -对了3个
- 4296849643607543 -对了3个
- 3174248439465858 -对了1个
- 4513559094146117 -对了2个
- 7890971548908067 -对了3个
- 8157356344118483 -对了1个
- 2615250744386899 -对了2个
- 8690095851526254 -对了3个
- 6375711915077050 -对了1个
- 6913859173121360 -对了1个
- 6442889055042768 -对了2个
- 2321386104303845 -对了0个
- 2326509471271448 -对了2个
- 5251583379644322 -对了2个
- 1748270476758276 -对了3个
- 4895722652190306 -对了1个
- 3041631117224635 -对了3个
- 1841236454324589 -对了3个
- 2659862637316867 -对了2个
找到那个唯一的16个数字。
Problem 186
现有一份繁忙的电话通讯系统记录的100万条记录:
| 序号 | 呼叫方 | 接收方 |
| 1 | 200007 | 100053 |
| 2 | 600183 | 500439 |
| 3 | 600863 | 701497 |
| ... | ... | ... |
在第n条记录中,呼叫方Caller(n) = S2n-1,接收方Called(n) = S2n,其中,S1,2,3,...生成自「滞后Fibonacci数生成器」:
当1 ≤ k ≤ 55时,Sk = [100003 - 200003k + 300007k3] mod 1000000。(译注:[ ]是取整数部分函数)
当56 ≤ k时,Sk = [Sk-24 + Sk-55] mod 1000000。
假如Caller(n) = Called(n)的话,就看作是用户拨错了号码,否则就当作是拨打成功。
从第一条记录开始,若X呼叫Y,或Y呼叫X,则X和Y是朋友。类似地,若X是Y的朋友,且Y是Z的朋友,那么X也是Z的朋友,如此下去,形成一条条关系链。
已知国家首相的电话号码是524287,那么从第一条记录开始,要经过多少次成功的拨打,才能使包括首相在内的99%的用户都是朋友呢?
Problem 187
「合数」就是至少含有两个质因数的整数,如,15 = 3 × 5, 9 = 3 × 3, 12 = 2 × 2 × 3。
在30以下有10个仅含有两个质因数的合数:4, 6, 9, 10, 14, 15, 21, 22, 25, 26。
设n < 108,且n是仅含两个质因数的合数,那么符合条件的n有多少个?
Problem 188
一个数字的b(正整数)次hyperexponentiation/tetration运算,可用a↑↑b或ba来表示,其递归定义为:
- a↑↑1 = a
- a↑↑(k+1) = a(a↑↑k)
例,3↑↑2 = 33 = 27,因此3↑↑3 = 327 = 7625597484987且3↑↑4大概等于103.6383346400240996×10^12。
请找到1777↑↑1855的后八位数。
Problem 189
看这个由64个小三角形组成的结构:

我们想给每一个小三角形涂上红、绿、蓝三种颜色之一,且相邻的两个三角形不能上同样的颜色,这就是上色的限制。若是两个三角形有公共边,则称这两个三角形相邻。
注意:有公共顶点的三角形不能看作是相邻的。
例如,上面的结构可以这么上色:
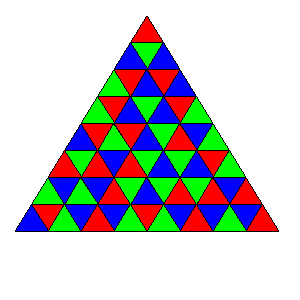
若着色方案C'是由着色方案C经过旋转或反射而来的,也将这两种方案看作是不同的,除非它们是完全一样的。
問:总共有多少种着色方案呢?
Problem 190
设Sm = (x1, x2, ... , xm)是一个正实数m元组,x1 + x2 + ... + xm = m且Pm达到最大值,Pm = x1 × x22 × ... × xmm。
例如,[P10] = 4112([ ]是指只取整数部分,截断小数部分)。
在2 ≤ m ≤ 15的范围中,Σ[Pm]的值是……?
Problem 191
某个奇怪的学校会定期给学风良好的学生颁发奖金。若他们「连续三天缺席」或「迟到两次」的话,他们的奖金就会被取消。
在n天的週期中,每个学生都有一条由三种字母组成的考勤记录,分别是L (迟到), O (准时), A (旷课)。
若以4天为週期,则有81种不同的记录,不过其中只有43种是能获奖的:
OOOO OOOA OOOL OOAO OOAA OOAL OOLO OOLA OAOO OAOA
OAOL OAAO OAAL OALO OALA OLOO OLOA OLAO OLAA AOOO
AOOA AOOL AOAO AOAA AOAL AOLO AOLA AAOO AAOA AAOL
AALO AALA ALOO ALOA ALAO ALAA LOOO LOOA LOAO LOAA
LAOO LAOA LAAO
若以30天为週期,那么能获奖的记录共有多少种?
Problem 192
设x为任意实数,现定义以d为分母上限时x的最优近似值是最简有理分数r/s,且s ≤ d,任何比r/s更接近x的有理数p/q都有一个大于d的分母q。
比如说,分母上限为20时√13的最优近似值是18/5,分母上限为30时则为101/28。
假设分母上限为1012,1 < n ≤ 100000,且n不为完全平方数,请求出所有√n的最优近似值的分母的和。
Problem 193
若正整数n不会被质数的平方整除的话,就叫做平方质数。
像1, 2, 3, 5, 6, 7, 10, 11都是平方质数,而4, 8, 9, 12都不是。
问:250以下有多少个平方质数?
Problem 194
假如我们在用A: 和B:
和B: 两种单元来构造图形,单元之间以竖直边相连在一起,像这幅图那样
两种单元来构造图形,单元之间以竖直边相连在一起,像这幅图那样 。
。
现以(a,b,c)表示一类复合图形,表示该图是用a个单元A和b个单元B构成的,用不超过c种颜色对图形中的点着色,并且任意两种相邻点之间的颜色都是不同的。
上面那幅复合图形的类型是(2,2,6),其实它同时也是(2,2,c)类型的,其中c ≥ 4。
设N(a,b,c)为(a,b,c)类型的图形的个数,则N(1,0,3) = 24, N(0,2,4) = 92928, N(2,2,3) = 20736。
请求出N(25,75,1984)的后8位数。
Problem 195
不妨将整数边长的且只有一个角为60度的三角形称作「60度三角形」吧,设r为该三角形的内接圆的半径。
已知当r ≤ 100时有1234种60度三角形。设T(n)为当r ≤ n时所有60度三角形的种数,则T(100) = 1234, T(1000) = 22767, T(10000) = 359912。
请求出T(1053779)。
Problem 196
用所有正整数建立如下的三角形数阵:
- 1
- 2 3
- 4 5 6
- 7 8 9 10
- 11 12 13 14 15
- 16 17 18 19 20 21
- 22 23 24 25 26 27 28
- 29 30 31 32 33 34 35 36
- 37 38 39 40 41 42 43 44 45
- 46 47 48 49 50 51 52 53 54 55
- 56 57 58 59 60 61 62 63 64 65 66
- . . .
每个正整数最多与8个数相邻。
三个质数被称为「质数三元组」,若其中某个质数与另外两个质数相邻。
举例说,在第二行,质数2和3是某三元组的成员。
在第8行,也有两个质数是某个三元组的成员,即29和31。
在第9行,只有一个质数是属于某个三元组的:37。
设S(n)为第n行中为某质数三元组的元素的所有质数的和,那么S(8)=60, S(9)=37。
已知S(10000)=950007619。
请求出S(5678027) + S(7208785)的值。
Problem 197
f(x) = ⌊230.403243784-x2⌋ × 10-9(⌊ ⌋是向下取整符号),而un的递归定义如下:
u0 = -1 , un+1 = f(un)
问:当n = 1012时,un + un+1为多少?
答案要精确到小数点后9位数。
Problem 198
设x为任意实数,现定义以d为分母上限时x的最优近似值是最简有理分数r/s,且s ≤ d,任何比r/s更接近x的有理数p/q都有一个大于d的分母q。
一般来说,每个实数在不同分母上限时的最优近似值是唯一的。不过还是例外的情况,如,当分母上限为6时,9/40有两个最优近似值1/4和1/5。若至少有一个分母上限使得x的最优近似值有两个,我们则称实数x是「模糊的」。显然,模糊的实数必然是有理数。
问:有多少个模糊的实数x = p/q,0 < x < 1/100且q不超过108呢?
Problem 199
在一个较大的圆里放入三个半径相等的圆,这些圆相切且内部的圆没有交错的地方。于是大圆内就产生了四个「空隙」,我们再循环地给这些空隙填入圆,使之与其它圆相切。
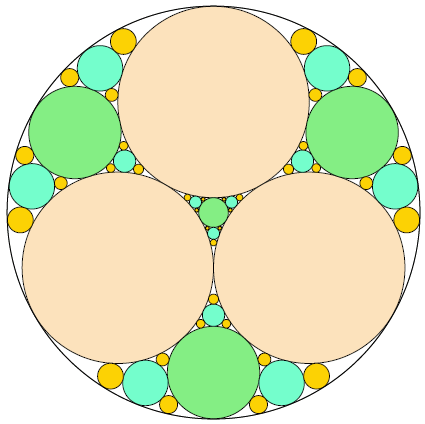
在每次循环中,在空隙中填入的圆必须是与其它圆相切的最大的圆,于是给下一次循环提供了更多的空隙。经过3次循环后的情况如上图所示,其中总共有108个空隙,并且这些空隙的总面积与整个大圆面积的比率为0.06790342,精确到小数点后8位数。
问:经过10次循环后,空隙的面积与大圆的面积的比率为多少?
答案要精确到小数点后8位数。
Problem 200
现定义「平方立方数」为具有如此形式的数字:p2·q3,其中,p和q是不同的两个质数。
例如,200 = 52·23,120072949 = 232·613。
前五个平方立方数是:72, 108, 200, 392, 500。
有趣的是,200是第一个这样的数,不论你改变它的哪一位数,都不可能将它变成质数,我们称这样的数是「抗质数化的」。已知第二个含有「200」字样的抗质数化的平方立方数是1992008。
请找出第200个包含「200」字样的抗质数化的平方立方数。
Problem 201
给定任意数集A,设sum(A)为A的所有元素的和。
现有数集B = {1,3,6,8,10,11}。
B有20个仅含3个元素的子集,它们的元素之和如下:
- sum({1,3,6}) = 10
- sum({1,3,8}) = 12
- sum({1,3,10}) = 14
- sum({1,3,11}) = 15
- sum({1,6,8}) = 15
- sum({1,6,10}) = 17
- sum({1,6,11}) = 18
- sum({1,8,10}) = 19
- sum({1,8,11}) = 20
- sum({1,10,11}) = 22
- sum({3,6,8}) = 17
- sum({3,6,10}) = 19
- sum({3,6,11}) = 20
- sum({3,8,10}) = 21
- sum({3,8,11}) = 22
- sum({3,10,11}) = 24
- sum({6,8,10}) = 24
- sum({6,8,11}) = 25
- sum({6,10,11}) = 27
- sum({8,10,11}) = 29
有些和重复出现了多次,有些是唯一的。
对于数集A,设U(A,k)为A的仅含k个元素的子集的各自元素的和中只出现过一次的和的集合。如上例中,U(B,3) = {10,12,14,18,21,25,27,29},且sum(U(B,3)) = 156。
现在再看这个有100个元素的集合S = {12, 22, ... , 1002},S总共有100891344545564193334812497256个仅含50个元素的子集。
请确定S的所有50个元素的子集的元素之和中只出现过一次的和的总和,即,求出sum(U(S,50))。
Problem 202
我们用三面镜子组合出了一个等边三角形,镜面是朝里的。顶点处都有一无穷小的空隙,这样激光束就能进出了。
将三个顶点标为A、B、C,激光束可以有两种方式进入,经过11次反射后从原来的入口返回:其中一种过程如下图,而另一种只是下图的反过程而已。
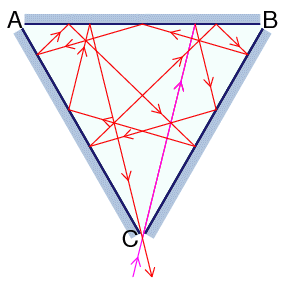
另外,激光束还有80840种方式从顶点C进入,经过1000001次反射后从C点射出。
那么从点C进入,经过12017639147次反射后从同一顶点射出的方式有多少种呢?(译注:我还没理解题目……可无视希望有人能指点一下我)
Problem 203
二项式系数nCk可排列成如下三角形的数列,即Pascal三角(或杨辉三角):
| 1 | ||||||||||||||
| 1 | 1 | |||||||||||||
| 1 | 2 | 1 | ||||||||||||
| 1 | 3 | 3 | 1 | |||||||||||
| 1 | 4 | 6 | 4 | 1 | ||||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||||||
可见Pascal三角的前8层总共有12个不同的数字:1, 2, 3, 4, 5, 6, 7, 10, 15, 20, 21, 35。
若正整数n无法被任一质数的平方整除,则称n为无平方因子数。以上12个数字中只有4和20不是无平方因子数,另外,那10个无平方因子数的和为105。
请求出Pascal三角前51层的所有不重复的无平方因子数的和。
Problem 204
没有大于5的质因数的正整数被称作Hamming数。
故头几个Hamming数有1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15。
已知不超过108的Hamming数有1105个。
另外,还有泛Hamming数(广义的Hamming数),若某正整数没有超过n的质因数,则称它为关于n的泛Hamming数。因此上述的几个Hamming数是关于5的泛Hamming数。
现在问你:不超过109的关于100的泛Hamming数有多少个?
Problem 205
Peter有九个四面骰(正四面体),每一面的点数分别是1, 2, 3, 4。
Colin有六个六面骰(立方体),每一面的点数分别有1, 2, 3, 4, 5, 6。
Peter和Colin各自掷骰,谁的点数总和最大就谁赢,点数一样就平局。
问:Peter赢的概率有多大呢?请将算出的答案精确到小数点后7位数(四捨五入)。
Problem 206
请找到这么一个数字,它的平方具有如下形式:
1_2_3_4_5_6_7_8_9_0
其中,「_」是指一位数。
Problem 207
对于某些正整数k,存在这么一个划分4t = 2t + k ,其中,4t, 2t, k都是正整数,且t是实数。
头两个这样的划分是41 = 21 + 2和41.5849625... = 21.5849625... + 6。
若划分中的t也是一个整数的话,就称之为完美划分。
对任意的m ≥ 1,令P(m)是k ≤ m的完美划分个数的倒数。因此,P(6) = 1/2。
如下是P(m)的一些值:
- P(5) = 1/1
- P(10) = 1/2
- P(15) = 2/3
- P(20) = 1/2
- P(25) = 1/2
- P(30) = 2/5
- ...
- P(180) = 1/4
- P(185) = 3/13
请找到最小的m,使得P(m) < 1/12345。
Problem 208
某个机器人做着一系列五分之一的圆(72°)的弧线运动,可以是顺时针或逆时针方向的,且无法在圆弧的端点上改变方向。
下图是一开始往北方经过25次弧线运动后使路径闭合的70932种情况中的一种:
假设这个机器人一开始面向北方,那么它经过70次弧线运动后回到起点的路径有多少种?(运动路径可以和以前的重合)
Problem 209
k输入二进制真值表即关于某些运算的所有从k个输入(二进制数字0[假]或1[真])到一个输出的映射。例如,以下为「与」运算(AND)和「异或」运算(XOR)的2输入二进制真值表:
| x | y | x AND y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| x | y | x XOR y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
而这次的问题是:有多少个6输入二进制真值表,τ,满足以下的逻辑运算式呢?
Problem 210
设集合S(r)为满足|x| + |y| ≤ r的整数坐标点集(x,y)。
再设O为原点(0,0),C为点(r/4,r/4)。
令N(r)为B点在集合S(r)中的个数,三角形OBC是钝角三角形,即是说其最大的内角α满足90°<α<180°。
因此,有N(4)=24,N(8)=100。
请问N(10,0000,0000)是多少?
Problem 211
设σ2(n)为正整数n的所有因数的平方和,如:
σ2(10) = 1 + 4 + 25 + 100 = 130
请求出小于6400,0000的正整数n中,所有σ2(n)为完全平方数的n的和。
Problem 212
一个对齐到坐标轴的立方体,可用参数{ (x0,y0,z0), (dx,dy,dz) }表示出来,这个立方体包含所有的点(X,Y,Z),x0 ≤ X ≤ x0+dx, y0 ≤ Y ≤ y0+dy, z0 ≤ Z ≤ z0+dz。这个立方体的体积为dx × dy × dz,一堆立方体的混合体积是他们的混合之后的总体积,若立方体之间有重叠的话,混合体积会比所有单独的立方体加起来的体积更小。
设C1,...,C50000为5,0000个对齐到坐标轴的立方体,Cn的参数表示为:
- x0 = S6n-5 mod 10000
- y0 = S6n-4 mod 10000
- z0 = S6n-3 mod 10000
- dx = 1 + (S6n-2 mod 399)
- dy = 1 + (S6n-1 mod 399)
- dz = 1 + (S6n mod 399)
其中,S1,...,S300000来自「滞后Fibonacci数生成器」:
- 当1 ≤ k ≤ 55时,Sk = [100003 - 200003k + 300007k3] mod 1000000
- 当56 ≤ k时,Sk = [Sk-24 + Sk-55] mod 1000000
于是,C1的参数表达是{(7,53,183),(94,369,56)},C2的则是{(2383,3563,5079),(42,212,344)},如此等等。
已知,前100个立方体C1,...,C100的混合体积是723581599。
问:这5,0000个立方体的混合体积是多少?
Problem 213
在一个30×30的网格中有900只跳蚤,刚开始每只跳蚤都单独呆在一个格子中。
每当铃铛被敲响时,每只跳蚤都随机地跳进相邻的格子中。(一般都有4种可能,除了某些呆在边缘和角落的跳蚤)
问题是:敲了50次铃之后,没有跳蚤的格子的个数的期望值是……?请将你的答案精确到小数点后6位数。
Problem 214
设φ是欧拉函数,即对于自然数n,φ(n)是n的与n互质的因数的个数。
通过欧拉函数,对每个正整数都能生成一串以1结尾的数字。
如,若以5开始,则可生成序列5,4,2,1。
如下是所有长度为4的序列:
- 5,4,2,1
- 7,6,2,1
- 8,4,2,1
- 9,6,2,1
- 10,4,2,1
- 12,4,2,1
- 14,6,2,1
- 18,6,2,1
其中只有两个数列是以质数开头的,这两个质数的和是12。
以4000,0000以下的数字生成的序列中长度是25的序列中,开头的所有质数的和是多少?
Problem 215
现在要用2×1和3×1的砖块来砌墙,为了让墙壁牢固一些,我们得避免构造出在上下层连续的缝隙。
如下图,这面9×3的墙壁是不符合安全规格的,出现的连续缝隙已由红线标记出来了:
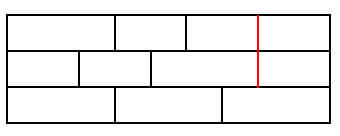
已知砌一面合格的9×3墙壁的合格方式有9种,简记为W(9,3) = 8。
请你算出W(32,10)的值。
Problem 216
有整数t(n) = 2n2-1且n > 1。
前几个这样的数有7, 17, 31, 49, 71, 97, 127, 161,而其中只有49 = 7×7和161 = 7×23不是质数。
若n ≤ 1,0000,那么这样的数中会有2202个是质数。
请问:当n ≤ 5000,0000时,有多少个t(n)是质数?
Problem 217
若一个k位的正整数的前⌈k/2⌉位数的和,和它的后⌈k/2⌉位数的和相等,则称它是「平衡数」。其中,⌈x⌉是表示對x向上取整,即取大于等于x的最小整数,故⌈π⌉ = 4,⌈5⌉ = 5。
所以,比如说,所有的回文数都是平衡数,像13722也是。
设T(n)为小于10n.的所有平衡数的和。那么有T(1) = 45, T(2) = 540, T(5) = 334795890。
请你求出T(47) mod 315的值。
Problem 218
有直角三角形的三边长分别为a=7, b=24, c=25,它的面积是84,84可被完美数6和28整除。
另外,它还是个朴素直角三角形,因为gcd(a, b)=1且gcd(b, c)=1。
还有,c是个完全平方数。
而符合以下两个条件的三角形就叫「完美直角三角形」:
- 它是个朴素直角三角形
- 它的斜边长是完全平方数
还有「超级完美直角三角形」:
- 它是完美直角三角形
- 它的面积能被完美数6和28整除
请问,斜边长c ≤ 1016的完美直角三角形中有多少个不是超级完美直角三角形?
Problem 219
设A和B为「比特串」(0和1的序列)。若B以A为开头,则称A是B的前缀。如,00110是001101001的前缀,但不是00111或100110的前缀。
一组大小为n的「无前缀相关性的」比特串,即,其中有n个不同的比特串,且任意两个比特串之间都不互为前缀。例如一组大小为6的比特串:
0000, 0001, 001, 01, 10, 11
现在假设每传送一个0要花费1便士,传送一个1要花费4便士。
则传送上述那组比特串总共要花费35便士,而这恰好是大小为6的一组无前缀相关性比特串在这个无理的价格标准下的最小花费了,我们把这个售价简写为Cost(6) = 35。
那么Cost(109) 是多少呢?
Problem 220
令D0为字符串"Fa",对于n ≥ 1,Dn根据以下方式由Dn-1衍生而来:
- "a" → "aRbFR"
- "b" → "LFaLb"
因此,D0 = "Fa", D1 = "FaRbFR", D2 = "FaRbFRRLFaLbFR",如此等等。
其实这些字符串可以被解释为某个计算机图形程序的指令:"F"表示前进1单位距离,"L"表示向左转90度,"R"则表示向右转90度,而"a"和"b"被忽略。而画笔的起始位置是(0,0),向着(0,1)的方向。
那么Dn就是就是一条奇特的n阶龙形曲线。如,下图的D10,每个"F"算一步,点亮的那个点(18,16)就是经过500步之后到达的位置。
那么画笔在D50上经过1012步后所在的位置是……?
请以「x,y」且不留空格的格式提交答案。
Problem 221
我们称正整数A为「亚历山大数」,若存在整数p, q, r,使得:
| A = p · q · r 且 |
|
= |
|
+ |
|
+ |
|
例如,630是一个亚历山大数(p = 5, q = -7, r = -18),它是第6个亚历山大数,而前6个亚历山大数是:6, 42, 120, 156, 420, 630。
请求出第15,0000个亚历山大数。
Problem 222
若管道的内半径为50mm,至少要设置多长的直线管道才能容纳21个半径分别为30mm, 31mm, ..., 50mm的球?
答案要求精确到微米(10-6 m),取四舍五入后的值。
Problem 223
若一个整数边长的三角形的三个边长a ≤ b ≤ c,満足以下条件,则称它是几乎锐角三角的:
a2 + b2 = c2 + 1
问:在周长不大于2500,0000的整数边长的三角形中有多少个是几乎锐角三角的?
Problem 224
若一个整数边长的三角形的三个边长a ≤ b ≤ c,満足以下条件,则称它是几乎钝角三角的:
a2 + b2 = c2 - 1.
问:在周长不大于7500,0000的整数边长的三角形中有多少个是几乎钝角三角的?
Problem 225
现有数列1, 1, 1, 3, 5, 9, 17, 31, 57, 105, 193, 355, 653, 1201 ...
它的定义方式为:T1 = T2 = T3 = 1且Tn = Tn-1 + Tn-2 + Tn-3。
可见,这个数列的任一项都不能被27整除。
我们还能知道,27是第一个符合这个条件的第一个奇数。
现在请你求出无法整除上述数列中任一项的第124个奇数。
Problem 226
牛奶果冻曲线即点集(x,y),0 ≤ x ≤ 1且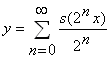 。
。
其中,s(x)为x 到其最近的整数的距离。
这条曲线和水平线包围出来的区域面积等于½,在下图中已经着色为粉红色:
令C是圆心为(¼,½),半径为¼的圆,在图中以黑线标出。
C所围得的牛奶果冻区域的面积是多少呢?
请把你的答案精确到小数点后八位数。
Problem 227
小游戏「奔跑」需要两个骰子和偶数个玩家。
玩家们围坐在桌子旁,游戏刚开始时,某两位在对角线上的玩家各自拥有一颗骰子。
每一轮,拿到骰子的玩家都要掷骰子,若掷到1,他就要把骰子交给他左边的那个玩家,若掷到6,就交给右边的那个玩家,否则骰子要继续保留在他那里。
当某位玩家拿到两个骰子时,游戏就结束了,那位玩家也就出局了。
在一个有100位玩家的奔跑游戏里,该游戏要结束需要的回合数的期望值是多少呢?
请把你的答案精确到小数点后10位数。
Problem 228
设Sn为实心的正n边形,其顶点vk (k = 1,2,…,n)的坐标是:
| xk = cos( 2k-1/n ×180° ) |
| yk = sin( 2k-1/n ×180° ) |
现定义「Minkowski和」S+T,为将形状S的每个点(x, y)加到T的每个点(u, v)上得到的图形,新图形的每一个点的坐标为(u, v) + (x, y) = (u+x, v+y)。
如,S3+S4为下面粉红色的六边形:
问:S1864 + S1865 + … + S1909有多少条边?
Problem 229
3600是一个奇特的数字,因为:
3600 = 482 + 1×362
3600 = 202 + 2×402
3600 = 302 + 3×302
3600 = 452 + 7×152
类似的数字,还有88201 = 992 + 2802 = 2872 + 2×542 = 2832 + 3×522 = 1972 + 7×842。
在1747年,数学家Euler就证明了正整数都能表示为两个平方数的和。而我们现在关心的是满足下面4种表示方式的数字n:
n = a12 + b12
n = a22 + 2 b22
n = a32 + 3 b32
n = a72 + 7 b72
其中,ak和bk都是正整数。
已知,在不超过107的数字中就有75373个这样的数字。
问:不超过2×109的数字中总共有多少个这样的数?
Problem 230
对于任意两串数字A和B,设FA,B为序列(A, B, AB, BAB, ABBAB, ...),其中每一项都是其前两项的连接。
接着,设DA,B(n)为FA,B中至少为n位数的第一项的第n位数。
例如,
令A=1415926535, B=8979323846,假设我们要求DA,B(35)。
FA,B的前几项是:
- 1415926535
- 8979323846
- 14159265358979323846
- 897932384614159265358979323846
- 14159265358979323846897932384614159265358979323846
于是,DA,B(35) 为第5项的第35位数,即9。
现在,令A为π的小数点后100位数:1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679
且令B为再接下来的100位数:8214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196
请求出∑n=0,1,...,17 10n×DA,B((127+19n)×7n)。
Problem 231
已知二项式系数10C3 = 120。
120 = 23 × 3 × 5 = 2 × 2 × 2 × 3 × 5且2 + 2 + 2 + 3 + 5 = 14。
因此该二项式系数的质因数分解的各项总和是14。
请求出二项式系数20000000C15000000的质因数分解中各项的总和。
Problem 232
两位玩家可轮流用一枚质地均匀的硬币来玩「赛跑游戏」。轮到玩家1时,他要抛一次硬币:若正面朝上,则他得到一分;若是反面朝上,则没有得分。轮到玩家2时,她要选定一个正整数T,然后掷T次硬币:若每次都是正面朝上,她就得到2T-1分;否则,她没有得分。游戏先由玩家1开始,第一个达到100分或以上的玩家胜出。
假设玩家2在每一轮中都选择一个使她的获胜率最大的数字T,那么玩家2赢的概率是多少呢?
请把你的答案精确到小数点后8位数。
Problem 233
设f(N)为经过点(0,0), (N,0),(0,N), (N,N)的圆上的具有整数坐值值的所有点的个数。
已知f(10000) = 36。
问:有多个小于等于1011的正整数N满足f(N) = 420呢?
Problem 234
现有定义,对于整数n ≥ 4,小于等于√n的最大质数称n的「小质平方根」,简记为lps(n);大于等于√n的最小质数称n的「大质平方根」,简记为ups(n)。
例如,lps(4) = 2 = ups(4),lps(1000) = 31,ups(1000) = 37。
另,对于整数n ≥ 4,若n仅能被lps(n)和ups(n)其中之一整除,则称n是「不完全可约数」。
已知不超过15的所有不完全可约数的和是30,它们有8, 10, 12。
15不是不完全可约的,因为它是lps(15) = 3和ups(15) = 5的整数倍。
再深入一点,不超过1000的共92个不完全可约数的和是34825。
那么,不超过999966663333的所有不完全可约数的和是……?
Problem 235
某算术几何数列的生成公式是u(k) = (900-3k)rk-1。
设s(n) = Σk=1...nu(k)。
请找到使s(5000) = -6000,0000,0000的r的值。
答案要精确到小数点后12位。
Problem 236
供应商'A'和'B'都为奢华的市场提供如下食品:
| 商品 | 'A' | 'B' |
|---|---|---|
| 白琼鱼子酱 | 5248 | 640 |
| 圣诞蛋糕 | 1312 | 1888 |
| 火腿肉 | 2624 | 3776 |
| 波尔图葡萄酒 | 5760 | 3776 |
| 香槟巧克力糖 | 3936 | 5664 |
虽然供应商已经极力地为食品做好保持工作,不过还是难免有食物变质的事情发生,即是说食物臭得不能吃了。
供应商们用两种数据来比较他们的工作情况:
- 这五种食品各自的变质率,即每种食品的变质个数除以每种食品的总数。
- 总变质率,即所有变质食品的个数除以所有食品的总数。
令供应商们感到惊讶的是,'B'的每各食品的变质率都比'A'的高,且比率都是一样的,为m>1;另外,'A'的总变质率比'B'的高,而比率也为m。
这样令人惊奇的发生情况有35种可能,其中最小的m为1476/1475。
那么m的最大值为多少呢?
请把你的答案化为具有u/v形式的最简分数。
Problem 237
设T(n)为在一个4 × n 的棋盘完全走上一遍的总的方式:
- 从左上角开始移动
- 每次只能向左 、右、上、下移动一个方格
- 每个方块只能走一次
- 移动在左下角结束
下图为在4 × 10的棋盘上的一种移动路径:

已知T(10)为2329,请求出T(1012) mod 108的值。
Problem 238
现在用一个叫做「嗙啷嗙啷唰」的伪随机数生成器生成一连串的数字:
| s0 | = | 14025256 |
| sn+1 | = | sn2 mod 20300713 |
然后将这些数字按顺序首尾相连,产生一个无限长的字符串 s0s1s2…即w = 14025256741014958470038053646…
对于任意正整数k,若w没有任何一个子字符串的每位数的和等于k,则定义p(k)为0;若至少有一个w的子字符串的每位数之和为k,则定义p(k) = z,z为这些子字符串中开始位置最靠前的位置数。
例如:
- 有子字符串1, 14, 1402, …它们每位数的和分别为1, 5, 7, …且开始位置都为1,故p(1) = p(5) = p(7) = … = 1。
- 有子字符串4, 402, 4025, …它们每位数的和分别为4, 6, 11, …且开始位置都为2,故p(4) = p(6) = p(11) = … = 2。
- 有子字符串02, 0252, …它们每位数的和分别为2, 9, …且开始位置都为3,故p(2) = p(9) = … = 3。
注意,子字符串025的开始位置是3,每位数的和为7,可是之前还有还有一个子字符串(开始位置是1)的每位数的和也是7,故p(7)等于1而不是3。
已知,当0 < k ≤ 103时∑ p(k) = 4742。
问:当0 < k ≤ 2·1015时,∑p(k)是多少?
Problem 239
标号为1到100的一百个光盘被随机地排列成一行。
问:刚好有22个标号为质数的光盘没有摆在与其标号相应的位置上的情况的概率是多少呢?
请将你的答案精确到小数点后12位数。
Problem 240
抛出五个六面骰(点数1到6)使得顶面点数之和为15的情况总共有1111种,例如:
- D1,D2,D3,D4,D5 = 4,3,6,3,5
- D1,D2,D3,D4,D5 = 4,3,3,5,6
- D1,D2,D3,D4,D5 = 3,3,3,6,6
- D1,D2,D3,D4,D5 = 6,6,3,3,3
那么抛出20个十二面骰(点数1到12)使得顶面点数之和为70的情况总共有多少种呢?
Problem 241
对于正整数n,设σ(n)为n的所有因子的和。如,σ(6) = 1 + 2 + 3 + 6 = 12。
而「完美数」,或许你已经知道,即符合σ(n) = 2n的数字n。
| 现在让我们定义某个正整数的「完美商」为 | p(n) | = |
σ(n)
n |
。 |
请求出所有不大于1018的符合这样条件的正整数n的和:p(n)能表示为k + 1⁄2,其中k是一个整数。
Problem 242
给定集合{1, 2, ..., n},定义f(n, k)为这个集合的仅有k个元素,且元素总和为奇数的子集的个数。例如,f(5, 3) = 4,因为集合{1, 2, 3, 4, 5}有4个仅含3个元素,且元素总和为奇数的子集,即:{1, 2, 4}, {1, 3, 5}, {2, 3, 4}, {2, 4, 5}。
当n, k, f(n, k)这三个值都为奇数时,我们就得到了「奇数三元组」[n, k, f(n,k)]。
当n ≤ 10时,总共有5个奇数三元组,即:[1, 1, f(1, 1) = 1], [5, 1, f(5, 1) = 3], [5, 5, f(5, 5) = 1], [9, 1, f(9, 1) = 5], [9, 9, f(9, 9) = 1]。
问:当n ≤ 1012时,总共有多少个奇数三元组?
Problem 243
若一个正分数的分子比它的分母小的话,就称这个分数为真分数。
对于任何一个分母d,总会有d-1个真分数。如,若d = 12则:
1/12 , 2/12 , 3/12 , 4/12 , 5/12 , 6/12 , 7/12 , 8/12 , 9/12 , 10/12 , 11/12
我们称一个不能不能再化简的分数为不可再约分数或最简分数。
另外,再来定义对于某个正分母d的不可约率为R(d),即对应的真分数中不可再约分数的比例。如,R(12) = 4/11。
其实,d = 12是使R(d) < 4/10的最小分母。
请找到使R(d) < 15499/94744的最小的分母d。
Problem 244
或许你已经听说过「十五数字重排游戏」了,现在,我们不用数字了,而是用红蓝的方块。
我们用各个方向的单词的首字母大写来表示方块的移动方向。例如,从最初的状态(S),经由LULUR的移动步骤,可达到状态(E):
| (S) |
 |
, (E) |
 |
对于每一系列移动步骤,它的校验和(checksum)的计算方法为:
checksum = 0
checksum = (checksum × 243 + m1) mod 100000007
checksum = (checksum × 243 + m2) mod 100000007
…
checksum = (checksum × 243 + mn) mod 100000007
其中,mk为移动步骤中第k个字母的ASCII编码数,表示四个移动方向的字母的对应ASCII码如下:
| L | 76 |
| R | 82 |
| U | 85 |
| D | 68 |
对于上面的移动步骤LULUR,它的校验和为19761398。
现在,要找到从状态(S)达到状态(T)的所有最短步骤,
| (S) |
 |
, (T) |
 |
并且求出这些最短步骤的校验和的总和。
Problem 245
我们称一个不能不能再化简的分数为不可再约分数或最简分数。
另外,再来定义对于某个分母d的不可约率为R(d),即对应的真分数中不可再约分数的比例。如R(12) = 4⁄11。
| 于是大于1的分母d的不可约率为 |
φ(d)
d - 1 |
,其中,φ为欧拉函数。 |
| 我们再定义大于1的整数n的可约系数为C(n) | = |
n - φ(n)
n - 1 |
。 |
| 因此任意质数p的可约系数为C(p) | = |
1
p - 1 |
。 |
请找到(1, 2×1011]区间中的所有合数n,并将其中符合C(n)为单分数的所有合数的和求出来。
Problem 246
对椭圆的一种构造方式如下:
取一个圆c,其圆心为M,半径为r,另外有一点G,线段GM < r,和点G还有圆c等距的所有点构成了一个椭圆。
该椭圆的构造过程如下所示:
现给定点M(-2000,1500)和点G(8000,1500),并且圆c的圆心为,半径为15000。和点G与圆c等距的所有点构成了椭圆e。
在椭圆e外有一点P,过点P作两条射线t1和t2与椭圆e相切,切点分别为R和S。
若点P的坐标值都是整数,那么有多少个点P使得∠RPS大于45°呢?
Problem 247
看看下面依条件1 ≤ x和0 ≤ y ≤ 1/x围成的区域。
设S1为那条曲线下能容纳的最大正方形,S2为除去被前者占用的区域后能容纳的最大正方形,如此下去,不断得到除去前面所有正方形所占区域后能容纳的最大正方形Sn。
设Sn的索引编码为二元组(左, 下),其表示了分别在Sn的左方和下方的正方形的个数。

上图用序号标出了这些正方形。S2的左方有一个正方形,其下方没有正方形,故它的索引编码是(1,0)。
于是可见,S32 的索引编码是(1,1),S50的也是这样。已知50是满足Sn的索引编码为(1,1)的最大的n。
问:满足Sn的索引编码是(3,3)的最大n值是……?
Problem 248
第一个使φ(n)=13!的数字是6227180929。
请求出第15,0000个这样的数。
Problem 249
设S为小于5000的所有质数的集合{2, 3, 5, ..., 4999}。
请求出这样的S的子集的个数:其元素之和为质数。
只要将答案的最右边16位数提交即可。
Problem 250
求:总共有多少个{11, 22, 33,..., 250250250250}的非空子集,其元素的和能被250整除?
请提交答案的最右边16个数字。
Problem 251
由正整数构成的三元组(a,b,c)若满足以下条件,则被称为Cardano三元组:
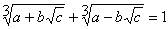
如,(2,1,5)是一个Cardano三元组。
已知,当a+b+c ≤ 1000时总共有149个Cardano三元组。
那么当a+b+c ≤ 1,1000,0000时有多少个Cardano三元组呢?
Problem 252
在平面上给定一些点,定义「凸边孔」为以给定的部分或所有点为顶点的凸多边形,且多边形中没有其它给定的点(除了顶点之外,其它给定点也可以坐落在其边上)。
例如,下图中有12个点,还有一些凸边孔。红色的那个七边形凸边孔的面积为1049694.5,那是在这12个点上能构造的最大的凸边孔所包围的面积:
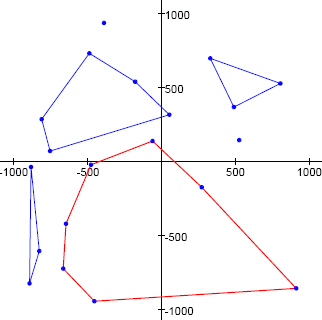
上述例子中的点的坐标是由以下的伪随机数生成器生成的,分别为(T2k![]() 1, T2k)的前20项,k = 1,2,…,20:
1, T2k)的前20项,k = 1,2,…,20:
| S0 | = | 290797 |
| Sn+1 | = | Sn2 mod 50515093 |
| Tn | = | ( Sn mod 2000 ) - 1000 |
即(527, 144), (![]() 488, 732), (
488, 732), (![]() 454,
454, ![]() 947), …
947), …
现在,给定以上面的伪随机数生成器产生的前500个点(T2k![]() 1, T2k),我们可以构造出来的最大凸边孔的面积是多少呢?
1, T2k),我们可以构造出来的最大凸边孔的面积是多少呢?
答案要精确到小数点后1位数。
Problem 253
有一位小孩子有一只「数字牵引车」,这辆玩具车由40块组件构成,每一块组件上都有一个数字,一旦将这些数字排起来,就是按顺序排列的数字1到40。
每天晚上,孩子的父亲都要捡起散落在游戏间里的玩具车组件,他随机地捡起各个组件,并且把它们按顺序摆放好。
这辆玩具车就是这样组装起来的,当组件一个个摆好并连接后就形成了一段段车身。
刚开始车身段的数目是零(还没有组件被摆放),然后逐渐上升到大概11或12,接着下降,直到最终只有1段(所有组件都按顺序摆好了)。
例如:
| 已摆放的组件数目 | 连成的车身段数目 |
| 12 | 1 |
| 4 | 2 |
| 29 | 3 |
| 6 | 4 |
| 34 | 5 |
| 5 | 4 |
| 35 | 4 |
| … | … |
设M为随机组装中出现的最大车身段数目,那么对于一个有10个组件的玩具车,M的各个值出现的情况种数如下:
| M | 情况总数 |
| 1 | 512 |
| 2 | 250912 |
| 3 | 1815264 |
| 4 | 1418112 |
| 5 | 144000 |
因此M的最可能数值是3,并且为M的值平均为385643⁄113400 = 3.400732,已精确到小数点后六位数。
已知对于有40个组件的玩具车来说,M的最可能数值是11,不过M的期望值是多少呢?
请把你的答案精确到小数点后六位数。
Problem 254
设f(n)为n的每位数的阶乘的总和,如,f(342) = 3! + 4! + 2! = 32。
设sf(n)为f(n)的每位数的总和,因此有sf(342) = 3 + 2 = 5。
设g(i)为满足sf(n) = i的最小正整数n,这样的话,虽然sf(342)等于5,sf(25)也等于5,不过可以证明g(5)等于25。
设sg(i)为g(i)的每位数的总和,故sg(5) = 2 + 5 = 7。
另外,可证明g(20) = 267且,当1 ≤ i ≤ 20时,∑sg(i) = 156。
问:当1 ≤ i ≤ 150时,∑sg(i)等于多少?
Problem 255
现定义正整数n的近似平方根为n的平方根四舍五入到整数的结果。
通过以下的方法(其实是将Heron法应用到整数计算中来了),我们可以求出n的近似平方根:
令d为n的位数,若d是奇数,则令x0 = 2×10(d-1)⁄2;若d是偶数,则令x0 = 7×10(d-2)⁄2。接着重复下面的计算:
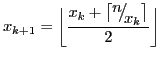
直到xk+1 = xk。
举个例吧,现在来找找n = 4321的近似平方根。n有4位数,故x0 = 7×10(4-2)⁄2 = 70。
由于x2 = x1,故计算到此为止。
于是,只经过了再次重复计算,我们就得到了4321的近似平方根,为66(实际的平方根是65.7343137…)。
这种方法要重复计算的次数出奇的少,比如说,我们找到5位数(10000 ≤ n ≤ 99999)的近似平方根的平均重复计算的次数是3.2102888889(已精确到小数点后10位数)。
若是使用这种方法,那么找到14位数(1013 ≤ n < 1014)的近似平方根的平均重复计算次数是多少呢?
请把答案精确到小数点后10位数。
注意:⌊x⌋ 和 ⌈x⌉ 分别表示对x「向下取整」和「向上取整」。
Problem 256
「榻榻米」是一种可用来铺满地板而不会发生重叠现象的矩形席子。
假设只有一种规格的榻榻米,其尺寸为1×2,这显然会对要铺榻榻米的房间的形状和大小有所限制。
对于这个问题,我们决定只考虑那些有整数边长的矩形房间,其长和宽分别为a, b,且其面积s = a·b为偶数。
我们说的「面积」指该房间的地板覆盖的面积,而且,为了不失一般性,我们规定a ≤ b。
铺排榻榻米时只须遵循一条规则:任何一个榻榻米的顶点都不能为四个榻榻米所共享。
例如,看看下面对于4×4的房间的两种铺排:
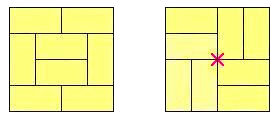
左边的铺排是合格的,而右边的则不行,中间那个红色的"X"指出了四个榻榻米共享的顶点。
由于这条规则,某些偶数面积的房间无法被铺上榻榻米:我们称这种房间为「榻榻米不合房间」。另外,我们定义T(s)为面积为s的榻榻米不合房间的种数。
最小的榻榻米不合房间的面积为70,尺寸为7×10。其它面积为70的房间都能铺上榻榻米,它们的尺寸分别是1×70, 2×35, 5×14。故T(70) = 1。
同样地,我们可以证明T(1320) = 5,因为面积为1320的榻榻米不合房间只有5种:
20×66, 22×60, 24×55, 30×44, 33×40
已知,1320是符合T(s) = 5的最小房间面积s。
请求出符合T(s) = 200的最小房间面积s。
Problem 257
有一个整数边长的三角形ABC的三边边长满足a ≤ b ≤ c,AB = c, BC = a, AC = b。该三角形的三条角平分线分别交其对边于点E, F, G。如图所示:
线段EF, EG, FG将该三角形分成了四个子三角形:AEG, BFE, CGF, EFG。可证明,对于这四个子三角形,面积△ABC/面积子三角形都是有理数。
特别的是,有些三角形的这些比值都是整数。
在周长不超过1,0000,0000的情况下,共有有多少个三角形ABC的所有面积△ABC/面积子三角形的值都是整数呢?
Problem 258
有个数列是这么定义的:
- gk = 1,若0 ≤ k ≤ 1999。
- gk = gk-2000 + gk-1999,若k ≥ 2000。
若k = 1018,则gk mod 20092010的值是多少?
Problem 259
一个正整数是「可达的」,若它是遵照如下规则而计算出的结果:
- 只用数字1至9,并且按顺序使用,每个数只用一次。
- 上述任意相邻的数字间可以相连(如,利用2, 3, 4可得到数字234)。
- 只允许使用四则运算符(加、减、乘、除)。
- 每个运算符可使用任意次数,不用也行。
- 不允许使用负号(即一元运算符「-」)。
- 可用任意对括号(可嵌套)来改变运算的顺序。
例如,42是可达的,因为(1÷23) × ((4×5)-6) × (78-9) = 42。
问:所有可达的正整数的和是多少?
Problem 260
现在我们来玩一种游戏,需要3堆石子和两个玩家。
在任一位玩家的回合,他都要从这几堆石子中移走一颗或更多的石子。不过,假如要从多于一堆石子中移走石子,那么在选择的每一堆中都要拿走相同的数量的石子。
换种方式说,玩家要选择一个大于0的数量N,并且移走:
- 一堆中的N颗石子,或
- 两堆中各N颗石子,总共2N颗,或
- 三堆中各N颗石子,总共3N颗。
这三堆石子的布置,可能会导致一种「必胜的布置」,使得第一位玩家肯定能胜出。
例如,(0,0,13), (0,11,11), (5,5,5)是必胜的布置,因为第一位玩家能马上把所有石子移走。
另外还可能会有「必输的布置」,第二位的玩家总是能赢,不管第一位玩家有什么动作。
例如,(0,1,2), (1,3,3)都是必输的布置,怎么合规则地移走棋子都无可阻挡第二位玩家得胜。
现在假设必输的布置为(xi,yi,zi),其中xi ≤ yi ≤ zi ≤ 100。
已知,∑(xi+yi+zi) = 173895。
假如xi ≤ yi ≤ zi ≤ 1000,那么∑(xi+yi+zi)的值是多少呢?
Problem 261
让我们称正整数k为「平方支点」,若存在一对整数m > 0和n ≥ k,使得不大于k2的(m+1)个连续的平方数的和,等于自(n+1)2开始的连续m个平方数的和:
较小的平方支点有:
- 4: 32 + 42 = 52
- 21: 202 + 212 = 292
- 24: 212 + 222 + 232 + 242 = 252 + 262 + 272
- 110: 1082 + 1092 + 1102 = 1332 + 1342
请求出不超过1010的所有平方支点的和。
Problem 262
如下方程表示的是某山地区域的连续地形分布情况,h表示任意一点(x, y)上的海拔:
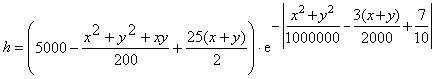
某只蚊子企图从A(200, 200)处飞到B(1400, 1400)处,并且其本身的坐标(x, y)总满足0 ≤ x, y ≤ 1600。
由于山路迂回,它一开始得先提升到某个点A',其海拔为f。接着,它保持着海拔f,绕过每一个障碍直到到达B处正上方的某一点B'。
首先,设fmin为这只蚊子从A处飞到B处,并不超出指定范围时,所能保持的最低海拔。
然后,请你求出这只蚊子保持以海拔fmin飞行时,点A'和点B'之间的最短路程。
答案要精确到小数点后三位数。
注意:为了方便,我们将上方的海拔函数在此再以利于转换为大多数编程语言的形式再重复一遍:
h=( 5000-0.005*(x*x+y*y+x*y)+12.5*(x+y) ) * exp( -abs(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7) )
Problem 263
来看看数字6,它有因子有:1, 2, 3, 6。从1到6的每个数字都能表示为6的不同因子的和:
1=1, 2=2, 3=1+2, 4=1+3, 5=2+3, 6=6。
若从1到n的数字都能表示成n的不同因子的和,则称n为「实用数」。
一对相邻且差为6的质数被称为「性感对」(因为sex是six,即6的拉丁文),已知首个性感对是(23, 29)。
或许我们还能找到「性感对三元组」,即有三个性感对,每对的第二个质数都是下一对的第一个数字。
若数字n同时满足:
- (n-9, n-3), (n-3,n+3), (n+3, n+9)为性感对三元组。
- n-8, n-4, n, n+4, n+8都是实用数。
请你找到前4个工程师的乐园的总和。
Problem 264
现考虑满足以下所有条件的所有三角形:
- 顶点都在边距为1的网格线的交点上。
- 外心为原点O。
- 垂心为点H(5, 0)。
周长不大于50的这样的三角形有9种,它们按周长升序排列如下图所示:
|
A(-4, 3), B(5, 0), C(4, -3) A(4, 3), B(5, 0), C(-4, -3) A(-3, 4), B(5, 0), C(3, -4) A(3, 4), B(5, 0), C(-3, -4) A(0, 5), B(5, 0), C(0, -5) A(1, 8), B(8, -1), C(-4, -7) A(8, 1), B(1, -8), C(-4, 7) A(2, 9), B(9, -2), C(-6, -7) A(9, 2), B(2, -9), C(-6, 7) |
 |
这9个三角形的周长的和精确到小数点后4位数为291.0089。
请求出周长不超过105的所有这样的三角形的周长之和。答案要精确到小数点后4位数。
Problem 265
2N个二进制单位可排列成环形,且顺时针N位的子序列都不一样。
如,N=3时可有两种旋转无关的排列:
在第一个排列中,所有3位的子序列按顺时针排列有:
000, 001, 010, 101, 011, 111, 110, 100
按顺时针连接所有数字,并以连续的0为前置,可把上述两种排列表示为23和29,成为其编码:
设S(N)为这些排列的编码的和,则有S(3) = 23 + 29 = 52。
现请求出S(5)。
Problem 266
能整除12的数有:1, 2, 3, 4, 6, 12。其中不超过12的平方根的最大者为3。
我们称n的因数中不超过n的平方根的最大因数为n的「伪平方根(PSR)」。
因此,PSR(3102) = 47。
设p是190以下所有质数的积,请求出PSR(p) mod 1016的值。
Problem 267
现在你有机会进行一次奇特的投资。
以1英磅作为本金,你可以选择一个固定的投资份额f,每个回合你抛一次硬币来决定你的资金是增长还是下降,如此进行1000回合即结束。
硬币若是正面朝上,则资金加倍返还;若是反面朝上,则资金流失。
例如,若f = 1/4,则第一回合你投资0.25贡磅,假如抛到的是正面,则获得0.5英磅,于是你总共有1.5英磅。接着,要投资0.375英磅,若抛得反面,则投资失败,你总共还有1.125英磅。
请优化f来使你在1000回合后获得至少拥有10,0000,0000英磅,这样,请问你成为亿万富翁的概率是多少呢?
所有的计算过程都要求精确(不能四舍五入),不过最终的答案只需要精确到小数点后12位就行了。
Problem 268
已知,1000以下总共有23个正整数,它们至少能被四个小于100的不同质数整除。
那么在1016以下总共有多少个这样的正整数数呢?
Problem 269
「根」是多项式P(x)关于方程P(x) = 0的x的解。
设Pn是系数皆为n的各位数的多项式。如,P5703(x) = 5x3 + 7x2 + 3。
可见:
- Pn(0)即n的最后一位数
- Pn(1)即n的各位数之和
- Pn(10)即n本身
设Z(k)为不超过k,并满足Pn至少有一个整数根的所有正整数n的个数。已知Z(100000) = 14696。
请求出Z(1016)。
Problem 270
一张具有整数尺寸N×N的方形纸片的某个角已经被对齐到直角坐标系的原点上及两条坐标轴x和y上。接着,我们按如下规则裁剪该纸片:
- 只在两条不同边上的具有整数坐标值的点之间作直线裁剪。
- 裁剪线之间不能交叉,但是可以共端点。
- 继续切割,直到不能再有合法的裁剪。
对称或旋转后相同的裁剪方案被视为不同的方案。设C(N)为裁剪N×N的纸片的所有方案种数。如C(1) = 2, C(2) = 30(如下图所示)。

问:C(30) mod 108的值是多少?
Problem 271
对于正整数n,设S(n)为所有大于1,小于n,且x3≡1 mod n的整数x的和。
当n=91时,x有8个值:9, 16, 22, 29, 53, 74, 79, 81。
故S(91)=9+16+22+29+53+74+79+81=363。
请求出S(13082761331670030)。
Problem 272
对于任意正数n,定义C(n)为大于1,小于n,且其立方除以n余1的整数的个数。
如,当n=91时,有8个这样的数,即:9, 16, 22, 29, 53, 74, 79, 81。故C(91)=8。
请求出不大于1011的所有C(n)=242的正整数n的和。
Problem 273
让我们思考一下这样的方程:a2 + b2 = N,0 ≤ a ≤ b,a, b, N都是整数。
当N=65时,该方程有两种解:
a=1, b=8或a=4, b=7。
设S(N)为当上述形式的方程的所有解的和,则S(65) = 1 + 4 = 5。
请求出∑S(N),其中,N为无平方因子数(不会被任一质数的平方整除),且N只能被这样的质数p整除,p = 4k+1,且p < 150。
Problem 274
对于任何大于1且与10互质的数字p,总存在唯一一个小于p的正「可除性因子」m,若p这能整除正整数n,那么m就能持p对以下关于n的函数值的可除性。
f(n) = (n不要最后一位数) + (n的最后一位数) × m
即是说,m是p的可除性因子,f(n)可被p整除,当且仅当n能被p整除。(当n远大于p时,f(n)会小于n,因而函数f的递归运用可作为测试p的可除性因子的方式。)
例如,113的可除性因子是34。
f(76275) = 7627 + 5 * 34 = 7797:76275和7797都能被113整除。
f(12345) = 1234 + 5 * 34 = 1404:12345和1404都不能被113整除。
已知,所有小于1000且与10互质的质数的可除性因子的和是39517。
问:所有小于107且与10互质的质数的可除性因子的总和是多少?
Problem 275
让我们定义一个「n阶平衡体」:
- 它是一个由n+1个同样的正方形格子组成的多格骨牌,分为「主体」(n格)和「底座」(1格)两部分。
- 底座的中心位置在(x = 0, y = 0)。
- 主体的位置的y坐标值大于0(因此底座总在最下面那格)。
- 平衡体的所有格子的中心的x坐标值的总和为0。
在计算平衡体的种数时,关于y轴对称的两个平衡体被视为同一种。例如,6阶的所有18种平衡体如下所示:

已知,10阶平衡体共有964种,15阶平衡体共有360505种。
问:18阶平衡体有多少种?
Problem 276
假设有具有整数边长a, b, c的三角形,a ≤ b ≤ c,那么整数边长的三角形(a,b,c)是朴素的,当且仅当gcd(a,b,c)=1。
问:在周长不超过1000,0000的整数连长的三角形中,有多少个朴素三角形?
Problem 277
有一种Collatz数列的变体是这么生成的,首先第一项是a1,接着:
- an+1 = an/3,若an能被3整除,这样的数值大下降现象我们就记为「D」。
- an+1 = (4an + 2)/3,若an除以3余1,这样的数值上升现象记为「U」。
- an+1 = (2an - 1)/3,若an除以3余2,这样的数值小下降现象记为「d」。
- 当生成的某一项为1时,数列就结束了。
只要给出一个数字,我们就能记下生成数列的过程。
如,若a1=231,则生成的数列为{an}={231,77,51,17,11,7,10,14,9,3,1},过程则记为「DdDddUUdDD」。
当然,也有别的数列的生成过程是以「DdDddUUdDD....」为开头的。如,若a1=1004064,则过程为「DdDddUUdDDDdUDUUUdDdUUDDDUdDD」。
已知,1004064是a1 > 106时,数列生成过程以DdDddUUdDD开头的最小的a1。
问:当a1 > 1015时,使生成过程以「UDDDUdddDDUDDddDdDddDDUDDdUUDd」为开头的第一项a1最小为……?
Problem 278
假设有一系列的整数1 < a1 < a2 < ... < an,有线性组合q1a1 + q2a2 + ... + qnan = b,qk ≥ 0且qk为整数。
注意,对于给定的一组整数ak,b不一定可以为任意值。如,若a1 = 5且a2 = 7,则不存在q1, q2使得b为:1, 2, 3, 4, 6, 8, 9, 11, 13, 16, 18, 23。
事实上,23是当a1 = 5且a2 = 7时,b的最大不可能数值。
于是我们称f(5, 7) = 23。
同样,已知f(6, 10, 15)=29, f(14, 22, 77) = 195。
若p < q < r < 5000,且p, q, r都是质数,则∑f(p*q,p*r,q*r)的值是多少呢?
Problem 279
在周长不超过108的整数边长的三角形中,有多少种三角形有至少一个整数度数的角呢?
Problem 280
有一只勤劳的蚂蚁在一个5×5的方形网格中随机走动,蚂蚁一开始在最中心的方格上,每次移动,这只蚂蚁都随机地走向相邻的一个格子,只要不超出网格,那么根据它所在的位置,它每次移动可以有2种、3种或4种可能的情况。
一开始,蚂蚁下方的所有格子中都分别有一颗种子。当它到达下方有种子的格子中时,就会扛上种子,接着只有当它去到上方的空格中时才会放下种子。
问:所有下方的种子被移到上方所需步骤的期望值是多少?
答案要精确到小数点后6位数。
Problem 281
你有一块Pizza饼(圆形的),它已经被等分成了m·n块,现在你想在每一小块上都添加一种配料。
设f(m,n)为使用m种配料(m ≥ 2),给n小块Pizza各添上一种配料的所有方案的数目(n ≥ 1)。
具有对称关系的两种方案被认为是不同的,而旋转后相同的方案则都只当作是一种方案。
因此,如f(2,1) = 1, f(2,2) = f(3,1) = 2, f(3,2) = 16。f(3,2)如下图所示:
请求出f(m,n) ≤ 1015的所有f(m,n)的和。
Problem 282
对于非负整数m, n,有Ackermann函数A(m, n):
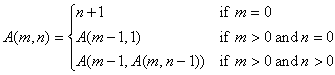
如,A(1, 0) = 2, A(2, 2) = 7, A(3, 4) = 125。
请求出( A(n, n) ) mod 148。
A(n, n) ) mod 148。
Problem 283
可见,边长分别为6, 8, 10的整数边长的三角形,其周长和面积皆为24,因此它的面积与周长之比为1。
另外,边长分别为13, 14, 15的整数边长的三角形的周长是42,面积为84,故其面积与周长之比为2。
请找出所有面积与周长之比不超过1000的所有整数边长的三角形,并把它们的周长之和算出来。
Problem 284
三位数376在十进制计数系统中有个特殊的性质,它的平方依然以这三个数结尾:3762 = 141376,不妨称这样的数为「平方稳定数」。
在其它进制计数系统中也有平方稳定数。例如在14进制中,三位数C37也是个平方稳定数:c372 = aa0c37,而且它的每位数的和为c+3+7=18(14进制),字母a, b, c, d分别被用来表示10, 11, 12, 13,就像16进制数一样。
当1 ≤ n ≤ 9时,14进制计数系统中所有n位的平方稳定数的所有位数的和为2d8(表示为十进制数即582),平方稳定数没有前置的0。
当1 ≤ n ≤ 10000时,14进制计数系统中所有n位的平方稳定数的所有位数的和为多少呢?结果请用14进制数表示,字母需为小写形式。
Problem 285
在一次游戏中,Albert要选择一个正整数k,接着在均匀分布的实数区间[0, 1]中随机取两个数字a, b。
然后他算出了(k·a+1)2 + (k·b+1)2的平方根,并四舍五入到整数,若结果等于k的话,他就能得k点分数,否则不得分。
例如,若k = 6, a = 0.2, b = 0.85,则(k·a+1)2 + (k·b+1)2 = 42.05。42.05的平方根是6.484...,而四舍五入到整数后为6。结果等于k,因此他得到6分。
可证明,若他玩10轮,分别选择k = 1, k = 2, ..., k = 10,则他的总得分的期望值精确到小数点后五位数是10.20914。
若是他玩105轮,分别选择k = 1, k = 2, k = 3, ..., k = 105,则他的总得分期望值精确到小数点后五位数又是多少呢?
Problem 286
Barbara是一位数学家兼篮球员。她发现,当她和篮筐的距离为x时能得分的机率刚好是(1 - x/q),其中,q为大于50的实数常数。
在每次训练中,她分别尝试从距离x = 1, x = 2, ..., x = 50的地方投篮,而且据记录发现,她总共得20分的机会恰好是2%。
请求出q,并将你的答案精确到小数点后10位数。
Problem 287
通过「四叉树」编码,我们可以将一幅2N×2N的黑白影像转换为一个比特串(由0和1组成),这个比特串的解读方法是从左到右的:
- 第一个比特处理整个2N×2N的图片区域;
-
"0"表示分割:将当前的2n×2n区域划分为四个2n-1
 2n-1的子区域,接下来的其它比特分别表示了对左上、右上、左下、右下四个区域的处理方法;
2n-1的子区域,接下来的其它比特分别表示了对左上、右上、左下、右下四个区域的处理方法; - "10"表示当前区域只含有黑色像素;
- "11"表示当前区域只含有白色像素。
现在来看看这个4×4的图像(能分割的地方已用彩色的点标记出来了):
这幅图能用这种比特串表示出来,像:"001010101001011111011010101010",长度为30;或"0100101111101110",长度为16,这也是表示该图像的最短比特串。
对于任意正整数N,设DN为一幅这样的2N×2N大小的图像:
- 其最左下角的像素坐标为x = 0, y = 0;
- 若像素坐标(x, y)满足(x - 2N-1)2 + (y - 2N-1)2 ≤ 22N-2,那么该像素是黑色的,否则该像素是白色的。
问:图像D24 ?经四叉树编码转换后的最短比特串的长度是多少?
Problem 288
对于任意质数p,定义N(p,q) = ∑n=0 ~ q Tn·pn。
其中,Tn由以下伪随机数生成器生成:
- S0 = 290797
- Sn+1 = Sn2 mod 50515093
- Tn = Sn mod p
设Nfac(p,q)为N(p,q)的阶乘,再设NF(p,q)为Nfac(p,q)的因式分解中因数p的个数。
已知,NF(3,10000) mod 320 = 624955285。
请求出NF(61,107) mod 6110的值。
Problem 289
令C(x,y)为过点(x, y), (x, y+1), (x+1, y), (x+1, y+1)的圆。
对于正整数m和n,设E(m,n)为由m·n个圆组成的图案:{ C(x,y): 0 ≤ x < m, 0 ≤ y < n, x和y都是整数 }。
在E(m,n)上的欧拉回路,即是一条经过每一条弧,且只经过一次的闭合路径。
我们可以在E(m,n)上找到很多种这样的路径,不过我们现在只关注那些没有出现交叉情况的欧拉回路:路径在交点上只是轻碰一下,但不会产生交叉。
下图展示的是E(3,3)和其中一条不交叉的欧拉回路:
设L(m,n)为E(m,n)上的欧拉回路的个数。如,L(1,2) = 2, L(2,2) = 37, L(3,3) = 104290。
请求出L(6,10) mod 1010的值。
Problem 290
若0 ≤ n < 1018,则有多少个数字n的各位数之和等于137n的各位数之和呢?
Problem 291
质数p被称作Panaitopol质数,若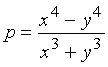 对于某对正整数x和y成立。
对于某对正整数x和y成立。
问:5×1015以下有多少个Panaitopol质数?
Problem 292
我们定义「毕达哥拉斯多边形」为具有如下性质的凸多边形:
- 至少有3个顶点。
- 任意三点间不共线。
- 每个顶点都的坐标值都是整数。
- 每条边的长度都是整数。
对于整数n,设P(n)为周长不超过n的毕达哥拉斯多边形的种数。
假如毕达哥拉斯多边形之间不能通过旋转或对称变成一样的,则认为它们是不同的种类的。
已知,P(4) = 1, P(30) = 3655, P(60) = 891045。求P(120)。
Problem 293
若一个正偶数是2的幂,或其不同的质因数为连续的质数项,则之为合理数。
而前12个合理数为2, 4, 6, 8, 12, 16, 18, 24, 30, 32, 36, 48。
若N是合理数,且M > 1,N+M是质数,那么就称M为N的伪幸运数。
如,630是合理数,因为其不同的质因数为连续的质数项2, 3, 5, 7。631之后的第一个质数是641,故630的伪幸运数是11。
同理,合理数16的伪幸运数是3。
请求出109以下所有合理数的不同伪幸运数之和。
Problem 294
对于任意正整数k,设d(k)为k在十进制下各位数的和,故d(42) = 4+2 = 6。
对于任意正整数n,设S(n)为小于10n并具有如下所有性质的正整数k:
- k可被23整除
- d(k) = 23
已知,S(9) = 263626, S(42) = 6377168878570056。
请求出S(1112) mod 109的值。
Problem 295
我们称两个圆形重叠的凸边包围的区域为「凸透镜孔」,若:
- 那两个圆的圆心坐标值都为整数。
- 那两个圆的交点有两个,并且这两个点的坐标值都为整数。
- 两圆形重叠的区域中不含坐标值都为整数的点。
现在来看看这些圆:
- C0: x2+y2=25
- C1: (x+4)2+(y-4)2=1
- C2: (x-12)2+(y-4)2=65
下图中含有这三个圆:
C0和C1之间,还有C0和C2之间,都形成了凸透镜孔。
我们称有序正实数对(r1, r2)为「凸透镜孔对」,若存在两个半径分别为r1和r2的圆,它们重叠形成了一个凸透镜孔。可见,上图说明了(1, 5)和(5, √65)都是凸透镜孔对。
设当0 < r1 ≤ r2 ≤ N时,所有不同的凸透镜孔对(r1, r2)的个数为L(N)。已知,L(10) = 30, L(100) = 3442。
求L(100 000)。
Problem 296
下图中有一个整数边长的三角形ABC,BC ≤ AC ≤ AB。
k 是∠ACB的角平分线,m为与三角形ABC的外接圆相切于点C的切线,直线n过点B与直线m平行,n和k的交点为E。
问:有多少种周长不超过10,0000的三角形ABC,其中BE的长为整数?
Problem 297
Fibonacci数列生成的每一项都是其前两项的和。
若以1和2为头两项,那么前十个Fibonacci数就是:1, 2, 3, 5, 8, 13, 21, 34, 55, 89。
每一个正整数都能以任意个不相邻且不相等的Fibonacci数列的项的和表示,并且这种对应是唯一的。如,100 = 3 + 8 + 89。
这样的表达式被称为该数字的Zeckendorf表达式。
对于任意正整数n,设z(n)为nZeckendorf表达式中Fibonacci数的个数。则z(5) = 1, z(14) = 2, z(100) = 3等等。
已知,在0 < n < 106的范围内,∑z(n) = 7894453。
求:在0 < n < 1017的范围内∑z(n)的值。
Problem 298
Larry和Robin正在玩一个记忆力游戏,这个游戏还和轮流出现的1到10的随机数字有关。每位玩家都最多只能「记住」5个之前出现过的数字,若出现的随机数已经在玩家的记忆里面了,那么玩家得1分;若是不在记里,则玩家要记住这个数字,若记忆中已经有5个数字了,就得去掉记忆中的另一个数字再加入新的数字。
两位玩家一开始都具有空白的记忆,两个玩家都要把没有记过的数字添加到记忆中,但是他们去除已记忆的数字时所采用的策略是不一样的:
- Larry的策略是去掉出现次数最少的数字。
- Robin的策略是去掉记忆中保留得最久的数字。
例如,游戏过程是这样的:
| 回合 | 随机数 | Larry的记忆 | Larry的得分 | Robin的记忆 | Robin的得分 |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 0 |
| 2 | 2 | 1,2 | 0 | 1,2 | 0 |
| 3 | 4 | 1,2,4 | 0 | 1,2,4 | 0 |
| 4 | 6 | 1,2,4,6 | 0 | 1,2,4,6 | 0 |
| 5 | 1 | 1,2,4,6 | 1 | 1,2,4,6 | 1 |
| 6 | 8 | 1,2,4,6,8 | 1 | 1,2,4,6,8 | 1 |
| 7 | 10 | 1,4,6,8,10 | 1 | 2,4,6,8,10 | 1 |
| 8 | 2 | 1,2,6,8,10 | 1 | 2,4,6,8,10 | 2 |
| 9 | 4 | 1,2,4,8,10 | 1 | 2,4,6,8,10 | 3 |
| 10 | 1 | 1,2,4,8,10 | 2 | 1,4,6,8,10 | 3 |
设Larry的得分为L,Robin的得分为R,请问回合数为50时|L-R|的期望值是多少?
答案要精确到小数点后8位数。
Problem 299
有四个具有整数坐标值的点A(a, 0), B(b, 0), C(0, c), D(0, d),0 < a < b且0 < c < d。
在线段AC上取一点P,使得三角形ABP, CDP, BDP都是相似三角形。
易证,只有当a=c时,这三个三角形才有可能是相似的。
因此,我们再规定a=c,现在我们要找到三元组(a,b,d),使得线段AC上至少存在具有整数坐标值的一点P,使得三角形ABP, CDP, BDP皆相似。
例如,若(a,b,d)=(2,3,4),则易证点P(1,1)即满足上述条件的点。注意,(2,3,4)和(2,4,3)仍旧会被认为是不同的,虽然点P(1,1)都符合这两种情况。
当b+d < 100时,共有92个三元组(a,b,d)满足上述条件。
当b+d < 10,0000时,共有320471个三元组(a,b,d)满足上述条件。
当b+d < 1,0000,0000时,又有多少个三元组(a,b,d)满足上述条件呢?
Problem 300
我们可以用一种非常简单的形式来描述各种蛋白质分子,即是将蛋白质看作是由疏水性元素(H)和极性元素(P)组成的,比如说HHPPHHHPHHPH。
蛋白质分子的朝向对此显得十分重要。比如说,HPP被认为是和PPH不同的,因此,若蛋白质分子有n种元素,那么就可能会有2n种不同的蛋白质。
当蛋白质处于自然状态时,H-H联结点的数目是尽可能大的,这能使分子的结构趋于稳定。于是,H元素总喜欢积聚于内部,而P元素则通常在外部。
当然,自然蛋白质是具有三维折叠状态的,不过在此处我们只考虑它们的二维折叠状态。
下图展示的是上面例子中的结构HHPPHHHPHHPH的两种可能的折叠方式(图中的红点即H-H联结点)。
左边的折叠方式中只有6个H-H联结点,因而它不会是自然发生的。而右边的折叠方式有9个H-H联结点,那显然是最佳的折叠方式。
假设H元素和P元素在任何位置出现的可能性是相等的,那么H-H联结点的数目在长度为8的随机蛋白质分子的最佳折叠中平均为850 / 28=3.3203125。
问:H-H联结点在长度为15的随机蛋白质分子的最佳折叠中的平均数目是多少?
上交的答案越精确越好,小数点后的数字要尽可能地多。
Problem 301
算筹游戏Nim是这么一个游戏:两个玩家轮流从几堆石子的任意一堆中拿走某个数量的石子,直到一个也不剩。
现在我们玩的是普通版本的Nim,具体的游戏规则如下:
- 一开始有三堆石子
- 玩家可以从任一堆中拿走任意正整数个石子
- 先拿不到石子的一方先输掉
用(n1,n2,n3)来表示Nim的这三堆石子的个数,要求设计出函数X(n1,n2,n3),其结果为:
- 0,即,若使用最佳策略,这一轮行动的玩家会输
- 非0,即,若使用最佳策略,这在轮行动的玩家会赢
如,X(1,2,3) = 0,因为不管这轮的玩家怎么拿,他的对手都可以使得剩下两堆一样多的石子,这样,先拿者的行动都可被后拿的模仿,于是先拿的必定输了。过程如下:
- 己方行动(1,2,1)
- 对方行动(1,0,1)
- 己方行动(0,0,1)
- 对方行动(0,0,0),对方赢
问:在230及以下共有多少个正整数n使得X(n,2n,3n) = 0?
Problem 302
正整数n是「强大的」,当且仅当n的任意质因数的平方为n的因数。
正整数n是「完美幂」,当且仅当n能表示为另一个正整数的幂。
正整数n是「Achilles数」,当且仅当n是强大的,但不是完美幂。例如,有Achilles数864和1800,864 = 25·33,1800 = 23·32·52。
我们还称正整数S为「强Achilles数」,若S和φ(S)都是Achilles数(φ为欧拉函数)。
如,864是个强Achilles数:φ(864) = 288 = 25·32。而1800不是,因为:φ(1800) = 480 = 25·31·51。
已知,在104以下共有7个强Achilles数,108以下则有656个。
那么在1018以下共有多少个Achilles数呢?
Problem 303
对于正整数n,設f(n)爲由不超过2的数字组成的最小正整数倍数。
因此,f(2)=2, f(3)=12, f(7)=21, f(42)=210, f(89)=1121222。
已知, 。
。
请求出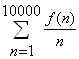 。
。
Problem 304
函数next_prime(n)能返回任意一个大于正整数n的最小质数。
数列{a(n)}有如下定义:
a(1) = next_prime(1014),且当n > 1时,a(n) = next_prime(a(n-1))
而Fibonacci数列是这么定义的:
f(0) = 0, f(1) = 1,且当n > 1时,f(n) = f(n-1) + f(n-2)
最后,数列{b(n)}为{f(a(n))}。
请求出1 ≤ n ≤ 100 000的范围内∑b(n)的值,请提交你的结果模1234567891011后的值。
Problem 305
令S为将十进制的正整数依序连接起来的无限长的字符串,即S = 1234567891011121314151617181920212223242...
显然,每个数字都会在S中出现无数次。
设f(n)为n在S中第n次出现时的开始位置。如,f(1)=1, f(5)=81, f(12)=271, f(7780)=111111365。
问:当1 ≤ k ≤ 13时,∑f(3k)的值是多少?
Problem 306
以下是一个关于组合数理论的游戏:
这个游戏需要两位玩家和一条有n个白色方格的带子,两人轮流行动。
每一回合,玩家要选择两个相邻的白色方格,并把它们涂成黑色。谁先无法做到这一步的就算谁输。
- 若n = 1,则一开始无法行动,所以第一个玩家自然是要输的。
- 若n = 2,则一开始只有一种合规则的行动,第二个玩家要输。
- 若n = 3,则一开始有两种符合规则的行动,不过都会导致第二个玩家输掉。
- 若n = 4,则一开始有三种符合规则的行动,第一个玩家只要将中间兩个方格涂上颜色就能赢。
- 若n = 5,则一开始有甲种符合规则的行动(如下图中的红色方格所示),可是无论如何,第二位玩家肯定会赢(蓝色方格为第二位玩家涂色的方格)。

因此,当1 ≤ n ≤ 5时,总共有有3种n的值使得第一位玩家必胜。
同样地,已知当for 1 ≤ n ≤ 50时,总共有40种n的值使得第一位玩家必胜。
问:当1 ≤ n ≤ 100,0000时,总共有多少种n的值使得第一位玩家必胜?
Problem 307
假设某个工厂制造的n个集成电路芯片中随机地出现了k种缺陷(一个芯片中可以有任意个缺陷,且在各个芯片中找到的缺陷都是不同的)。
设p(k,n)为有某个芯片至少含有3种缺陷的概率。如,p(3,7) ≈ 0.0204081633。
请求出p(20000, 1000000)精确到小数点后10位数的值。
Problem 308
每个由编程语言「分数语言」编写的「分数程序」都包含着一张分数表。
某部「分数虚拟机」的内在状态用一个正整数来表示,其初始值被设定为某个值。分数程序在每次循环中,都将其内在状态乘以第一个能使结果为整数的分数,并将结果设为新的内在状态。
例如,John Horton Conway写了一个能生成质数的,由14个分数组成的分数程序:
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
。 |
设定该程序的内在状态的初始值为整数2,该程序的后续循环产生了如下序列:
15, 825, 725, 1925, 2275, 425, ... , 68, 4, 30, ... , 136, 8, 60, ... , 544, 32, 240, ...
在序列中出现过的2的幂有22, 23, 25, ...
可见,所有这些2的幂的指数都为质数,且这些指数都是按顺序出现的!
如果某人用上面的分数程序来解决ProjectEuler.net的Problem 7(找到第10001个质数),那么该程序要经过多少次循环才能产生2第10001个质数呢?
Problem 309
在「交叉梯子」这个经典的问题中,某小巷中有两个长度分别为x和y的梯子靠在相对的两面墙上。另外,我们还得知两条样子的交叉点距地面的高度h,接着我们得求出小巷的宽度w。
在此,我们只考虑这四个变量都为正整数的情况。
例如,若x = 70, y = 119, h = 30,则我们可以算出w = 56。
已知,对于整数x, y, h,当0 < x < y < 200时,只有5个三元组(x,y,h)能给出w的整数解:(70, 119, 30), (74, 182, 21), (87, 105, 35), (100, 116, 35), (119, 175, 40)。
对于整数x, y, h,当0 < x < y < 1000000时,使w有整数解的三元组(x,y,h)有多少个呢?
Problem 310
Alice和Bob两人正在玩平方算筹游戏Nim Square。
Nim Square的规则就和一般的有三堆石子的算筹游戏Nim一样,不过玩家每次只能从一堆石子中移走平方数颗石子。
我们用有序三元组(a,b,c)来表示三堆石子的数量。
已知,若0 ≤ a ≤ b ≤ c ≤ 29,则第二位玩家必输的情况共有1160种。
若0 ≤ a ≤ b ≤ c ≤ 10,0000,那么第二位玩家必输的情况有多少种呢?
Problem 311
现有整数边长凸四边形ABCD,1 ≤ AB < BC < CD < AD。线段BD的长为整数,点O为BD的中点,线段AO的长也为整数。
若AO = CO ≤ BO = DO,则称四边形ABCD为「双倾整数边长四边形」。
如,下面的四边形就是一个双倾整数边长四边形:
AB = 19, BC = 29, CD = 37, AD = 43, BD = 48, AO = CO = 23
设B(N)为满足AB2+BC2+CD2+AD2 ≤ N的双倾整数边长四边形的种数。
已知,B(10000) = 49,B(100,0000) = 38239。求B(100,0000,0000)。
Problem 312
- 一个1阶的Sierpiński图(S1)是一个等边三角形。
- Sn+1为摆放Sn的三个副本使得每一对副本之间都有一个共同的夹角所形成的图形。
设C(n)为环绕着遍历Sn的每个顶各一次的所有方案总数。
如,C(3) = 8,各种方案如下:
另外,已知:
- C(1) = C(2) = 1
- C(5) = 71328803586048
- C(10 000) mod 108 = 37652224
- C(10 000) mod 138 = 617720485
请求出C(C(C(10000))) mod 138的值。
Problem 313
有一种华容道游戏,一个单元只能水平或垂直移动到空格中,这个游戏的目的是把网格中最左上角的红色单元移动到最右下角。这个游戏刚开始时,空格总是在最右下角。例如,下图说明了在2×2的网格中如何经过5步就通过了游戏:
设S(m,n)为通过网格为m×n的游戏所需的最小移动次数。如,S(5,4) = 25。
已知当p < 100,且p为质数时,总共有5482种网格满足S(m,n) = p2。
问,当p < 106且p为质数时,有多少种网格满足S(m,n) = p2?
Problem 314
月球已经被开发了,而且人们能够免费使用其上的土地,不过有一个棘手的问题需要解决:我们得在人们要活动的地方建造围墙,可是那样做的耗费是极大的。每个国家都分得了一块500m×500m的土地,不过它们只会占用要进行活动的地方。分配所得的地面被251001根杆子每隔一米划分成一个个方形区域,建造的围墙必须是由一段段由一个杆子到另一个杆子的直直的墙围成的。
当然一些较大的国家建造了2000m的围墙,包围的区域有25,0000m2。在这些国家中,大芬威格公国的预算很紧,其尊贵的程序员,即你,被要求计算怎样的形状才能使包围区域的面积和围墙长度的比值最大。
你已经在草稿纸上作了初步的计算,得知用2000m的围墙包围25,0000m2的区域,包围区域面积/围墙长度的比值是125。
虽然这样做是不可能的,不过假如能想到更好的办法就好了:若你在这块方形的土地中作一个内切圆,则圆的面积为π×2502m2 ,周长则是π×500m,这样包围区域面积/围墙长度的值也是125。
然而,若你在方形土地的四个角上各去掉一个边长为75m, 75 m, 75√2m的三角形区域,那么土地的面积就变成了238750m2,围墙的长度就变成了1400+300√2m,这样,包围区域面积/围墙长度值就是130.87,显然这方法非常棒。
请你继续求出包围区域面积/围墙长度的最大值,并把答案精确到小数点后8位数。
Problem 315

Sam和Max被要求把两部数字时钟变成两部「数字根」时钟。
数字根时钟,即是一步步算出数字根的数字时钟。
当给时钟输入了一个字数之后,它就会开始慢慢地,计算每一步的答案,直到得到最终的答案。
例如,若给时钟输入数字137,它就会显示:"137" → "11" → "2",然后黑屏,等待另一个数字的输入。
每个数字都需要由一些发光单元组成:三个水平的(上、中、下),和四个竖直的(左上、右上、左下、右下)。
数字"1"由右上和右下两个发光单元组成,数字"4"由中、左上、右上、右下四个发光单元组成,数字"8"则需要所有七个发光单元组成。
时钟只有在开/关发光单元时消耗能量。发光单元显示"2"需要5次转换,而显示"7"只需要4次转换。
Sam和Max设计了两个不同的数字根时钟。
假设Sam的时钟被输进了数字137:时钟显示了"137",然后整个画面都黑掉,接着另一个数字"11"又显示出来,然后再次黑屏,最终显示数字"2",过一会黑屏结束。
上面的例子中,输入数字137,Sam的时钟需要:
| "137" | : | (2 + 5 + 4) × 2 = 22次转换("137"亮/暗) |
| "11" | : | (2 + 2) × 2 = 8次转换("11"亮/暗) |
| "2" | : | (5) × 2 = 10次转换("2"亮/暗) |
总共40次转换。
Max的时钟则不太一样。他的时钟不会让屏幕上的数字所部消失,而是只关闭那些显示下一个数字时不需要的发光单元。
以输入137为例吧,Max的时钟需要:
|
"137" |
: |
2 + 5 + 4 = 11次转换("137"亮) 7次转换(关闭显示"11"不需要的发光单元) |
|
"11" |
: |
0次转换("11"已经亮着了) 3次转换(前面的"1"暗掉,后面的"1"暗掉下半部分,上半部分和"2"有重叠) |
|
"2" |
: |
4次转换(开启其它显示"2"所需的发光单元) 5次转换("2"整个暗掉) |
总共需要30次转换。
显然,Max的时钟比Sam的更省能量。
现在,这两部时钟都被输入了107和2×107之间的所有质数。
请求出两人的时钟的发光单元所需转换次数的差值。
Problem 316
假设有由无穷个随机数字连接成的数字p = p1 p2 p3 ...,每个随机的数字都等概率地取自集合{0,1,2,3,4,5,6,7,8,9}。
可见,p能对应一个实数0.p1 p2 p3 ....,那么在区间[0,1)上等概率取一个实数,相当于在集合{0,1,2,3,4,5,6,7,8,9}中等概率地取无穷个数字。
对于任意具有d位数的正整数n,设k为pk, pk+1, ...pk+d-1按顺序在n中出现的最小的开始位置,再设g(n)为k的期望值。可证明,g(n)总是有限的数字,并且总会是一个整数,很奇妙吧?
例如,若n = 535那么对于p = 31415926535897....,可得k = 9;对于p = 355287143650049560000490848764084685354...,可得k = 36;如此等等,还能求出g(535) = 1008。
已知 ,请求出
,请求出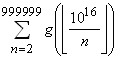 的值。
的值。
提醒: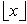 表示对x向下取整。
表示对x向下取整。
Problem 317
一个鞭炮在离平地100m的高空爆炸了,产生了大量细小的碎片,这些碎片向各个方向飞去,它们的初速度都为20m/s。
假设这些碎片的移动都不受空气阻力,仅受到统一的重力加速度g=9.81m/s2。
请计算这些碎片落地之前的移动范围占据的空间大小(m3)。答案要精确到小数点后四位数。
Problem 318
来看看实数√2+√3,当我们算出它的平方次幂时,可见:
- (√2+√3)2 = 9.898979485566356...
- (√2+√3)4 = 97.98979485566356...
- (√2+√3)6 = 969.998969071069263...
- (√2+√3)8 = 9601.99989585502907...
- (√2+√3)10 = 95049.999989479221...
- (√2+√3)12 = 940897.9999989371855...
- (√2+√3)14 = 9313929.99999989263...
- (√2+√3)16 = 92198401.99999998915...
- ...
看来随着次数的增大,结果的小数部分开头连续的9的个数是不会下降的。
其实,可证明(√2+√3)2n的小数部分随着n的增大,越来越接近1。
再来考虑下具有√p+√q形式的实数,其中p和q都是正整数,且p < q,且(√p+√q)2n的小数部分随着n的增大而越来越接近1。
设C(p,q,n)为(√p+√q)2n的小数部分开头连续的9的个数,N(p,q)为满足C(p,q,n) ≥ 2011的最小的n。
问:当p+q ≤ 2011时,∑N(p,q)的值是多少?
Problem 319
x1, x2,..., xn为具有n项的数列:
- x1 = 2
- 当1 < i ≤ n时,xi-1 < xi
- 当1 ≤ i, j ≤ n时,(xi) j < (xj + 1)i
长度为2的这样的数列只有5个,分别是:{2,4}, {2,5}, {2,6}, {2,7}, {2,8}。长度为5的则有293个,其中三个如下:
{2,5,11,25,55}, {2,6,14,36,88}, {2,8,22,64,181}
若将长度为n的这样的数列的个数表示为t(n),则有t(10) = 86195和t(20) = 5227991891。
请求出t(1010) mod 109的值。
Problem 320
设N(i)为能够使n!被(i!)1234567890整除的最小整数n。
再设S(u) = ∑N(i),10 ≤ i ≤ u。
已知,S(1000) = 614538266565663。
求S(100,0000) mod 1018。
Problem 321
在一排2n + 1个格子的两端上分別有n個红色的筹码和n个蓝色的筹码,中间隔着一个空格子。当n = 3时,如下图:

我们可以把某个筹码直接移到相邻的一格上,或者让它越过相邻的筹码到达没有筹码的空格上。

设M(n)为将两种颜色的筹码的位置调换过来所需的最小移动步骤,即是要把红色的全部移到右边,蓝色的全部移到左边。
已知,M(3) = 15,它恰好是个三角形数。
若是把M(n)为三角形数的n组成数列,那么这个数列的前5项是1, 3, 10, 22, 63,且它们的和为99。
请你找出这个数列的前40项的和。
Problem 322
设T(m, n)为当n ≤ i < m时,能被10整除的二项式系数iCn的个数(i, m, n都是正整数)。
已知T(109, 107-10) = 989697000,求T(1018, 1012-10)。
Problem 323
设y0, y1, y2,...是随机生成的一系列无符号32位整型数。(即是说,0 ≤ yi < 232)
xi是一递归生成的序列的某一项:
- x0 = 0
- xi = xi-1 | yi-1, i > 0(|是「或」运算符)
显然,最终总会有一个整数N,使得xi = 232-1(转换为二进制时每位都是1),i ≥ N。
请求出N的期望值。
答案要精确到小数点后10位数。
Problem 324
设f(n)为能用2×1×1的砖块砌一个3×3×n的柱子的不同方案的总个数。
你可以随意旋转砖块,我们视旋转后相同或对称的两种柱子是不同的。
如,若q = 100000007:
- f(2) = 229
- f(4) = 117805
- f(10) mod q = 96149360
- f(103) mod q = 24806056
- f(106) mod q = 30808124
请求出f(1010000) mod 100000007的值。
Problem 325
有个游戏需要两位玩家和两堆石子。当轮到某位玩家时,他必须从石子较多的那一堆中移走一定数量的石子,并且石子的个数必须为另一堆石子的数个的正整数倍。
即,令有序数对(6,14)表示数量为6的较小的一堆石子,和数量为14的较多的另一堆石子的布置,那么第一位玩家要从更大的那堆石子中拿走6颗或12颗石子。
最先把某堆石子完全移走的玩家得胜。
「必胜的布置」会使第一位玩家必定能够胜出,例如,(1,5), (2,6), (3,12)是必胜的布置,因为第一位玩家能立刻把较大的那堆石子移光。
「改输的布置」则会使得不管第一位玩家怎么行动,第二位玩家总会赢。例如,(2,3)和(3,4)是必输的布置,第一位玩家的任何行动都会为第二位玩家提供必胜的布置。
设S(N)为当0 < xi < yi ≤ N时所有必输的布置(xi+yi)的个数。已知S(10) = 211, S(104) = 230312207313。
请求出S(1016) mod 710的值。
Problem 326
数列{an}的递归定义为: 。
。
因此{an}的前10项为:1, 1, 0, 3, 0, 3, 5, 4, 1, 9。
设f(N,M)为满足如下条件的数对(p, q)的个数:
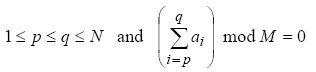
可证明,f(10,10)=4,相应的数对为(3,3), (5,5), (7,9), (9,10)。
我们还已知,f(104,103)=97158。请求出f(1012,106)。
Problem 327
某三个房间是通过自动门连接的:
每扇自动门都需要一张门卡才能进行操控。一旦你进入了房间,门就会自动关闭,并且开门用的那张门卡也从此失效了。在起始处(Start)有一个无限制分发门卡的机器,可是起始处和每个房间里都有监测器,假如你手上拿着超过三张门卡或者地上有未使用过的门卡,那么所有自动门都会永久关闭。然而幸好每个房间都有一个箱子,你可以安全地把任意数量的卡片储存在里面,留备后用。
如果你仅仅打算只经过每一扇门一次,那么当你去到第3个房间时就会把门卡用光,结果永远被锁在那间房子里了!
不过假如你好好地利用那些储存箱,你还是有可能逃出去的。例如,你可以用第一张门卡进入1号房间,然后往储存箱中放一张,接着再用第三张打开门回到起始处,在机器那再拿三张门卡,那么你就可以再到1号房间拿回储存箱里的卡,那样你又有三张门卡了,于是你就能连续通过剩下的自动门了。这种方法总共要使用6张门卡。
我们还可以用123张门卡通过6个房间,同时门卡的最大携带数目是3。
设C是任何时候能携带的门卡的张数上限,设R是要通过的房间的数目,再设M(C,R)为此时要通过所有房间所需的最少门卡数。
如,M(3,6)=123, M(4,6)=23;当3 ≤ C ≤ 4时,∑M(C,6)=146。
已知当3 ≤ C ≤ 10时,∑M(C,10)=10382。
请求出当3 ≤ C ≤ 40时∑M(C,30)的值。
Problem 328
我们要从{1, 2, ..., n}之中猜一个数字,每猜一次的花费就等于猜的那个数(猜中时不计),可能得到的回答会有三种:
- 「你猜的数比答案小。」
- 「没错,你猜对了!」
- 「你猜的数比答案大。」
对于任意给定的n,一个最佳策略会把花费降到最低(即考虑最糟糕的情况下的最小花费)。例如:
若n=3,那么我们最好的做法显然就是猜是不是「2」,回答会立刻使我们找到答案(这样总花费是2)。
若n=8,那么我们或许得选用「二分搜索」策略:首先猜「4」,如果答案大于4,那么我们就还要继续猜一到两次;假设第二次我们猜「6」,若答案依然大于6,那么我们就要猜多一次,才能知道答案是7还是8,于是我们当然是猜「7」了,这样就知道在最糟糕的情况下,总花费为4+6+7=17。
我们还能改善当n=8时的最坏情况下的花费,只要一开始猜「5」就可以了。
假如接下来的回答是答案大于5,那么接着应该猜「7」,这样我们就必定能知道答案了(总花费为5+7=12)。
若回答是答案小于5,那么接着就猜「3」,假如答案小于3,则猜「1」,于是总花费为5+3+1=9。(译注:总是考虑最糟的情况,不认为自己那么容易一下就能猜中剩下的两个数中哪个是答案。)
由于12>9,故使用这种策略能使得在最坏的情况下花费最多为12。这种策略比先前那种「二分搜索」策略好多了,与其它的策略相比只可能有过之而无不足。
不过我们只是描述了一下最佳策略对于n=8的情况。
设C(n)为专门应付至于n的使用如上所述的最佳策略在最坏的情况下的最小花费。显然,C(1) = 0, C(2) = 1, C(3) = 2, C(8) = 12。
已知,C(100) = 400,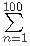 C(n) = 17575。
C(n) = 17575。
请求出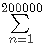 C(n)。
C(n)。
Problem 329
Susan有一只「质数青蛙」宠物,她的这只青蛙正在500个标号为1到500的格子上跳来跳去。这只青蛙每次只能向左或向右跳一格,并且往两边跳的概率都是相等的,另外它怎么都跳不出1到500的范围。(假如它跳到了末端,那么它下一次就会自动跳向旁边仅有的格子。)
当这只青蛙在号码为质数的格子上时,在跳向下一个格子前它有2/3的概率会呱呱地叫出「P(质数)」,1/3的概率叫出「N(非质数)」。
假定青蛙的初始位置在每一个格子上的概率都是相等的,并且Susan听它呱呱地叫了15次,那么她听到「PPPPNNPPPNPPNPN」的概率是多少呢?
请将你的答案用最简真分数p/q的形式表示。
Problem 330
无穷实数数列{a(n)}对于整数n的定义如下:

例如:
| a(0) = |
|
+ |
|
+ |
|
+ ... = e - 1 |
| a(1) = |
|
+ |
|
+ |
|
+ ... = 2e - 3 |
| a(2) = |
|
+ |
|
+ |
|
+ ... = |
|
e - 6 |
其中,e = 2.7182818... 为欧拉常数。
| 可证明,a(n)可以表示为 |
|
,A(n)和B(n)为整数。 |
| 例如,a(10) = |
|
。 |
请求出A(109) + B(109) mod 7777,7777的值。
Problem 331
某个N×N的方形棋盘上放满了N×N个棋子,所有的棋子都是一面黑色的,另一面白色的。
每一回合,你都可以选择一个棋子,并且翻转同一行和同一列上的所有棋子:于是总共翻转了2×N-1个棋子,当所有棋子都是白色那一面朝上时,游戏便结束了。下图展示了一个用5×5的棋盘玩这个游戏的过程:

可证明,上面那个游戏所需的最小回合数是3。
棋盘最左下角的格子的坐标是(0,0),最右下角的格子的坐标是(N-1,0),最左上角的则是(0,N-1)。
令CN 为对于N×N的棋盘的棋子的初始设置:
坐标为(x,y)的棋子若满足 ,则黑色那一面朝上,否则白色那一面朝上。上图显示了C5的情况。
,则黑色那一面朝上,否则白色那一面朝上。上图显示了C5的情况。
设T(N)为完成初始设置为CN的游戏的最小回合数,当游戏无解时则为0。
我们之前已经说明了T(5)=3,现在还已知T(10)=29, T(1 000)=395253。
请求出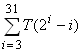 。
。
Problem 332
一个球面三角为球面上三个大圆弧两两相交形成的由三个顶点和三条弧围成的形状。

设C(r)为以(0,0,0)为圆心,半径为r的球体。
设Z(r)为C(r)表面上坐标值皆为整数的点组成的集合。
设T(r)为以Z(r)中的在C(r)表面不共弧的点为顶点构成的球面三角的集合。
设A(r)为为T(r)中球面三角的面积的最小值。
已知A(14)精确到小数点后6位数后为3.294040。请求出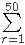 A(r)精确到小数点后6位数后的值。
A(r)精确到小数点后6位数后的值。
Problem 333
所有正整数都能被分割成各部分都为2ix3j的几部分,其中i, j ≥ 0。
让我们来仅考虑那些各部分之间不能相互整除的分割吧。
例如,分割17 = 2 + 6 + 9 = (21x30 + 21x31 + 20x32)中由于2能整除6而不符合上述要求。分割17 = 16 + 1 = (24x30 + 20x30)也不符合要求,因为1能整除16。对于17只有唯一的合格分割8 + 9 = (23x30 + 20x32)。
许多正整数都有不止一种合格分割,11是第一个拥有两种合格分割的正整数:
- 11 = 2 + 9 = (21x30 + 20x32)
- 11 = 8 + 3 = (23x30 + 20x31)
设P(n)为n的合格分割种数,则P(11) = 2。
现在我们只看看那些只有一种合格分割的质数q吧,如P(17) = 1。
已知,小于100的所有P(q)=1的质数q的总和为233。
请求出小于100,0000的所有P(q)=1的质数q的总和。
Problem 334
在柏拉图的天堂里,有无数个碗排成了一条直线,每个碗中有有限颗豆子或没有豆子。
有位小孩在那里玩着一个游戏,这种游戏只有一种操作:从任意一个碗中取出两颗豆子,并把这两颗豆子分别放到旁边的两个碗中。只有当每个碗中都有一颗或零颗豆子时,游戏才会结束。
例如,假如有两个相邻的碗中分别有2颗和3颗豆子,其它碗中都没有豆子,那么以下8次操作就能完成这个游戏:
现在你得知了如下两个数列:
| t0 = 123456 |
| ti = |
 |
|
|||||||||||||||
| 其中,⌊x⌋表示对x向下取整, | |||||||||||||||||
| ⊕为异或运算符 |
| bi = ( ti mod 211) + 1. |
数列{bi}的头两项是b1 = 289和b2 = 145。
若是上述两个相邻的碗中分别有b1和b2颗豆子,则需要3419100次操作才能完成游戏。
若是有连续摆放的碗1500个,每个碗中的豆子数量分别是b1, b2,..., b1500,并且其它碗都是空的,那么需要多少次操作才能完成游戏呢?
Problem 335
Peter每当感觉无聊的时候,都会将几个碗摆成一圈,并在每个碗中放一颗豆子。接着,他把其中一个碗中的所有豆子拿出来,并按顺时针方向把手中的豆子一颗一颗地放到其它碗中。他会从最后放豆子的那个碗开始不断地重复这个过程,直到每个碗中再次都只有一颗豆子。例如,若有5个碗的话,他会这么做:

因此,当有5个碗时,Peter要重复15次操作才能使每个碗恢复到初始状态。
设M(x)为有x个碗时需要的重复操作次数。已知M(5) = 15,M(100) = 10920。
请求出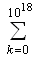 M(2k+1) mod 79的值。
M(2k+1) mod 79的值。
Problem 336
某辆火车要按顺序运输四个车厢ABCD,可是,有时火车要装载车厢时会发现它们的顺序不对。
为了重新调整好顺序,得把这些车厢转轨到一个大的转车台上,当车厢在转车台的特定位置脱钩后,火车就拖着仍然连着的车厢离开转车台,剩下的车厢就在转车台上进行180度旋转,然后重新和火车连接,如此重复,而且必须尽量在最少的步骤内调整好。
有些顺序,如ADCB,很容易调整:车厢从A和D之间分离,接着车厢DCB旋转180度就好了。
不过,列车长Simple Simon因为个人的效率问题而不太受欢迎,他总是先把车厢A调好正确的位置,再调整车厢B,接着是车厢C、D等等。
若是有四个车厢,这时不妨称对Simon来说最糟糕的顺序为「最复杂的顺序」,它就是顺序DACB和DBAC,这两种顺序都要让他花5次旋转才能搞定(虽然说最快只需要3次旋转)。他调整车厢DACB的步骤如下:
已知,若有6个车厢,那么Simon可能会面对24种最复杂的顺序,而按照词法顺序其中第十个是DFAECB。
若是有11个车厢,那么按词法顺序,Simon可能面对的第2011个最复杂的顺序是什么呢?
Problem 337
{a1, a2,..., an}为具有n项的整数数列:
- a1 = 6
- 当1 ≤ i < n时,φ(ai) < φ(ai+1) < ai < ai+1(φ为欧拉函数)
设S(N)为满足an ≤ N的如上数列的个数。如,S(10) = 4,有:{6}, {6, 8}, {6, 8, 9}, {6, 10}。
另外还已知S(100) = 482073668且S(10000) mod 108 = 73808307。
请求出S(2000,0000) mod 108的值。
Problem 338
现在有一张整数尺寸的w×h的方格纸,每个方格的边长都为1。
假如我们沿着方格的边把这张纸裁剪成两片,然后重新调整一下它们的位置,就能得到一个新的不同尺寸的矩形。
例如,用一张9×4的方格纸,我们可以通过裁剪和调整,做出18×2、12×3、6×6的矩形:
类似地,还能把9×8的方格纸做成18×4和12×6的矩形。
对于w和h,设F(w,h)为用w×h的方格纸能做出的矩形的种数。如,F(2,1) = 0, F(2,2) = 1, F(9,4) = 3, F(9,8) = 2。
注意,原来w×h的矩形并不包括在F(w,h)内,还有,w×h和h×w的矩形将被视为同一种类。
对于整数N,令G(N)为满足0 < h ≤ w ≤ N的所有F(w,h)的和。
已知G(10) = 55, G(103) = 971745, G(105) = 9992617687。请求出G(1012) mod 108的值。
Problem 339
「接着他前往一个小山谷,山谷中有一条小河流过,四周郁郁葱葱的,河的两边都有一片平坦的草地。他看见,一边的草地上有一群白羊,另一边则有一群黑羊。每当有一头白羊咩咩叫时,就会有一头黑羊走到另一边,变成白羊;每当有一头黑羊咩咩地叫时,也会有一头白羊走到另一边变成黑羊。」——摘自en.wikisource.org
假设刚开始每群羊都有n头,每一头羊都等可能地会是下一头要叫的羊。当一头羊叫完,且另一头羊走到另一边后,故事主人公Peredur或许会移走几头白羊,以使他最终能得到的黑羊的个数最大化。设E(n)为Peredur使用最佳策略时最终能得到的黑羊个数的期望值。
已知E(5)精确到小数点后六位数后为6.871346。
请求出E(10000)精确到小数点后6位数后的值。
Problem 340
对于恒定的整数a, b, c,疯狂函数F(n)的定义如下:
- 当n > b时,F(n) = n - c
- 当n ≤ b时,F(n) = F(a + F(a + F(a + F(a + n))))
另外,再设S(a, b, c) = 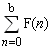 。
。
例如,若a = 50, b = 2000, c = 40,则F(0) = 3240, F(2000) = 2040。
已知,S(50, 2000, 40) = 5204240。
请求出S(217, 721, 127)的最后9位数。
Problem 341
Golomb自描述序列{G(n)}是满足n恰好出现了G(n)次的唯一升序自然数序列。{G(n)}的前几项如下所示:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| G(n) | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 6 | 6 | 6 | 6 | … |
已知,G(103) = 86, G(106) = 6137,且当1 ≤ n < 103时∑G(n3) = 153506976。
问:当1 ≤ n < 106时∑G(n3)的值是多少。
Problem 342
来看看数字50吧,502 = 2500 = 22 × 54,故φ(2500) = 2 × 4 × 53 = 8 × 53 = 23 × 53。(φ为欧拉函数)
因此2500是平方数,且φ(2500)是立方数。
若1 < n < 1010,则所有满足φ(n2)是立方数的n的和是多少呢?
Problem 343
对于任意正整数k,可通过如下方式构造ai=xi/yi形式的有穷数列:
- a1 = 1/k,当i = 1时;
- ai = (xi-1+1)/(yi-1-1)的最简分数,当i > 1时。
当ai为某个整数n时,数列就结束了。(即,当yi=1时。)设f(k) = n。
如,若k = 20,有数列:
1/20 → 2/19 → 3/18 = 1/6 → 2/5 → 3/4 → 4/3 → 5/2 → 6/1 = 6
故f(20) = 6。
另外,已知f(1) = 1, f(2) = 2, f(3) = 1;当1 ≤ k ≤ 100时,∑f(k3) = 118937。
若1 ≤ k ≤ 2×106,则∑f(k3)的值是多少呢?
Problem 344
下面要介绍的是一个从N.G. de Bruijn所创的「银元游戏」演变过来的新游戏:
在一排方格子中放有几枚硬币,一个格子最多放一枚硬币。其中只有一枚叫做「银元」的硬币,它的价值无法估计。两位玩家轮流进行操作,在每一轮,玩家只能采取一次「常规操作」或一次「特殊操作」。
「常规操作」即选取一枚硬币,将它向左移动一个或多个方格,且该硬币不能被移出这一排方格,也不能叠在其它硬币上或跨过其它硬币。
另外,玩家还能选择进行「特殊操作」,即把最左边的那枚硬币收起来,而当无法进行常规操作时,玩家只能被强制执行特殊操作。
最先把银元收起来的玩家得胜。
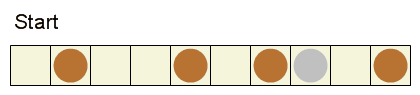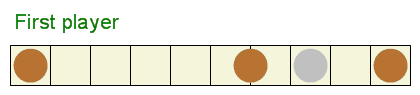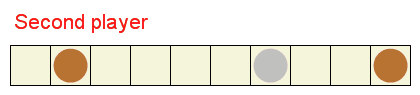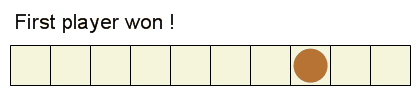
一个必胜布置就是无论第二位玩家怎么操作,第一位玩家必然可以得胜的硬币初始布置。
设W(n,c)为当有n个格子、c个无价值的硬币和一个银元时,必胜布置的个数。
已知W(10,2) = 324, W(100,10) = 1514704946113500。
请求出W(1000000, 100) mod 1000036000099的值。(「半素数」1,0000,3600,0099 = 100,0003 × 100,0033)。
Problem 345
现定义「矩阵和」为矩阵中在每一行和每一列上都为最大值的数字的和。例如,下面的矩阵的矩阵和是3315( = 863 + 383 + 343 + 959 + 767):
7 53 183 439 863
497 383 563 79 973
287 63 343 169 583
627 343 773 959 943
767 473 103 699 303
现在请你求出如下矩阵的矩阵和:
7 53 183 439 863 497 383 563 79 973 287 63 343 169 583
627 343 773 959 943 767 473 103 699 303 957 703 583 639 913
447 283 463 29 23 487 463 993 119 883 327 493 423 159 743
217 623 3 399 853 407 103 983 89 463 290 516 212 462 350
960 376 682 962 300 780 486 502 912 800 250 346 172 812 350
870 456 192 162 593 473 915 45 989 873 823 965 425 329 803
973 965 905 919 133 673 665 235 509 613 673 815 165 992 326
322 148 972 962 286 255 941 541 265 323 925 281 601 95 973
445 721 11 525 473 65 511 164 138 672 18 428 154 448 848
414 456 310 312 798 104 566 520 302 248 694 976 430 392 198
184 829 373 181 631 101 969 613 840 740 778 458 284 760 390
821 461 843 513 17 901 711 993 293 157 274 94 192 156 574
34 124 4 878 450 476 712 914 838 669 875 299 823 329 699
815 559 813 459 522 788 168 586 966 232 308 833 251 631 107
813 883 451 509 615 77 281 613 459 205 380 274 302 35 805
Problem 346
7这个数字很特别,因为把7转换成二进制数是111,转换为六进制数是11(即,710 = 116 = 1112)。这即是说,7在被转换成大于1进制的数字时至于有两种进制下是循环单位(译注:完全由1构成的数)。
我们将像7这样的数称为「强循环单位」,可证明,在50以下总共有8个强循环单位,即:{1,7,13,15,21,31,40,43}。
另外,已知1000以下的所有强循环单位的和为15864。
请求出1012以下所有强循环单位的和。
Problem 347
不大于100且只质因数中只有2和3的最大整数是96,96=32×3=25×3。
对于两个不相等的质数p和q,设M(p,q,N)为不大于N,且质因数中只含p和q的最大正整数。并定义M(p,q,N)=0,若不存在这样的正整数。
如,M(2,3,100)=96。M(3,5,100)为75而不是90,因为90的质因数有2 ,3, 5。
同样地,M(2,73,100)=0,因为不存在不大于100且质因数中只含2和73的正整数。
设S(N)为所有不同的M(p,q,N)的和,那么S(100)=2262。
请求出S(1000,0000)。
Problem 348
许多数字都可以表示为一个平方数和一个立方数的和,还有一些还能用多种平方数、立方数对的和表示。
现在来看看大于1的,而且能刚好能用4种一个平方数和一个立方数的和表示的「回文数」吧。
例如,回文数5229225恰好能用4种平方数、立方数对的和表示:
- 22852 + 203
- 22232 + 663
- 18102 + 1253
- 11972 + 1563
请你求出这样的最小的5个回文数的和吧。
Problem 349
某只蚂蚁在一个布满黑白格子的网格上移动,这只蚂蚁总是只能朝向四个基本方向(上、下、左、右),并且按照以下规则不断移动到相邻的格子:
若它在黑格子上,它就把这一格变成白格子,接着它逆时针旋转90度,然后前进一格。
若它在白格子上,它就把这一格变成黑格子,接着它顺时针旋转90度,然后前进一格。
若刚开始整个网格都是白色的,那么这只蚂蚁移动1018次后会有多少个黑格子呢?
Problem 350
一个长度为n的列表即n个自然数。例如有(2,4,6), (2,6,4), (10,6,15,6), (11)。
最大公约数(gcd),即能整除列表中所有数字的最大自然数。如:gcd(2,6,4) = 2, gcd(10,6,15,6) = 1, gcd(11) = 11。
最小公倍数(lcm),即能被列表中所有数字整数的最小自然数。如:lcm(2,6,4) = 12, lcm(10,6,15,6) = 30, lcm(11) = 11。
设f(G, L, N)为满足gcd ≥ G且lcm ≤ L的长度为N的列表,如:
- f(10, 100, 1) = 91
- f(10, 100, 2) = 327
- f(10, 100, 3) = 1135
- f(10, 100, 1000) mod 1014 = 3286053
请求出f(106, 1012, 1018) mod 1014的值。
Problem 351
一个n阶的六边形果园为边长为n的六边形,其内部分布着由点构成的一个个三角区域。下图为一个5阶果园。

以绿色背景高亮的点为被离中心点更近的点遮挡而无法在中心点处观察到的点。可见,在5阶的门边形果园中有30个点被挡住了。
设H(n)为n阶六边形果园中站在中心点无法观察到的点的数目。
则H(5) = 30, H(10) = 138, H(1 000) = 1177848。
求H(1,0000,0000)。
Problem 352
有25头羊,其中每一头都将被用于测试一种罕见的病毒,据说这种病毒会影响到这群羊的总数的2%。另外还有一台高精度兼高灵敏度的PCR测试仪,该仪器可用于测试血液样本,判断病毒反应呈阳性还是阴性,不过使用该仪器会耗费不少的时间和金钱。
由于花费过高的原因,主管医师决定,与其直接进行25次测试,不如按以下的方法来测试:
羊群被分为5个小组,每组5头羊,每组羊的所有血液样本都被混合到一起,只做一次测试。那么:
- 若结果是阴性的,则认为那组羊都是对病毒有耐受能力的。
- 若结果是阳性的,则继续对那组羊的每一头都重新取样进行单独的测试,经过5次另外的测试后发现受影响的个体。
鉴于这种病毒对每头羊的感染率仅仅为0.02,因此对第一组的测试结果是:
- 阴性的(不再需要额外的测试),概率为0.985 = 0.9039207968。
- 阳性的(需要额外的5次测试),概率为1 - 0.9039207968 = 0.0960792032。
所以每一组所需的测试次数的期望值是1 + 0.0960792032 × 5 = 1.480396016。
结果是,所有5组羊平均只需要通过1.480396016 × 5 = 7.40198008次测试就能把对病毒呈阳性和阴性的羊隔离开来,这样就能节省70%的花费!
虽然我们刚才谈到的测试方案看起来很有效率,不过它还是能被进一步改进的(总是设想测试仪器足够精确灵敏,并且混合不同的血液不会起反效果),即是这样:
- 一开始我们混合所有25头羊的血液样本做一次测试,已知结果呈阴性的概率约为60.35%,那样的话就不需要再测试了;只有当结果为概率约39.65%的阳性时才需要额外测试。
- 若我们知道5头羊一组中至少有一头羊被感染了,那么当前4头羊的测试结果为阴性时,就没必要为剩下的最后一头羊做测试了(它肯定是被感染了)。
- 我们能够尝试分不同的组,每组中有不同数量的羊,使得总的测试次数的期望值最小。
为了缩小众多的可能性的范围,我们要在策划最节省资金的方案时加上一条限制:每当我们以混合的血液样本开始做测试时,所有为该样本提供血液的羊的状况都必须能够完全呈现出来(即是说,在为另一组羊做测试之前,得弄明白当前组的每头羊对病毒是呈阳性还是阴性)。
对于当前的例子来说,最节省资金的方案(我们称之为最佳策略)所需的平均测试次数仅为4.155452!设T(s,p)为用最佳策略检测s头羊对病毒的反应结果所需的平均测试次数,其中p为任一个体受感染的概率。故,若结果精确到小数点后6位数,则T(25, 0.02) = 4.155452, T(25, 0.10) = 12.702124。
请求出∑T(10000, p),p=0.01, 0.02, 0.03, ... 0.50。
答案要精确到小数点后6位数。
Problem 353
月球可被描述为一个球心为(0,0,0),半径为r的球体C(r)。
假设月球上,即C(r)表面上在坐标值都为整数的点上,都有一个监察站。在(0,0,r)上的监察站被称为北极站,在(0,0,-r)上的被称为南极站。
所有监察站之间都通过球体表面经过它们的最短弧线连接着,在两个监察站之间来回是很危险的,假设两个监察站之间的路程为d,那么危险程度就是(d/(π·r))2。若要经过两个以上的监察站,那么危险程度就是所有要经过相邻两个监察站的危险程度的和。
直接从北极站到南极站,总路程为πr,相应的危险程度为1。虽然从北极站经过(0,r,0)上的监察站到达南极站的路程一样,可是危险程度会小得多:(1/2·πr/(πr))2+(1/2·πr/(πr))2=0.5。
设在C(r)上从北极站到南极站的最小危险程度为M(r)。
已知M(7)精确到小数点后10位数是0.1784943998,求∑M(2n-1),1 ≤ n ≤ 15。
答案要精确到小数点后10位数。
Problem 354
假设某个蜜蜂巢的每一个蜂室都是边长为1的正六边形。
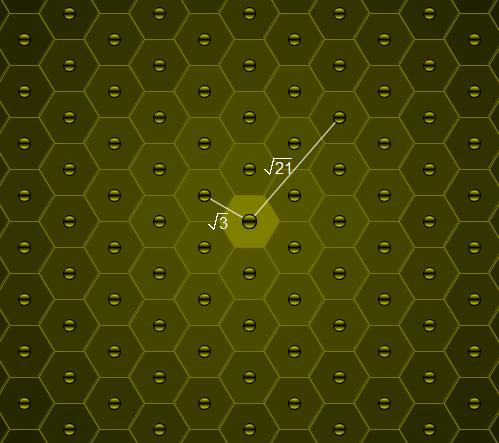
其中有一个蜂后专用的特殊蜂室。
对于任意正实数L,设B(L)为与蜂后所在的蜂室相距L的蜂室的个数(距离为正六边形的中心之间的距离)。不妨假设这个蜂巢足够大,大到我们可以假设任意的距离。
例如,B(√3) = 6, B(√21) = 12, B(1,1111,1111) = 54。
请求出距离不超过5·1011且满足B(L) = 450的距离L的个数。
Problem 355
设Co(n)为{1, 2, ..., n}的子集中满足元素间两两互质的集合的所有元素之和的最大值。
如,Co(10)为30,相应的集合是{1, 5, 7, 8, 9}。
已知,Co(30) = 193,Co(100) = 1356。请求出Co(200000)。
Problem 356
g(x) = x3 - 2n·x2 + n,设an为多项式方程g(x) = 0的最大的实数根。如,a2 = 3.86619826...。
请求出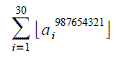 的最后8位数。
的最后8位数。
提醒: 表示对a向下取整。
表示对a向下取整。
Problem 357
现在来看看30的因子:1, 2, 3, 5, 6, 10, 15, 30。
可见,对于30的每个因子d ,d+30/d是一个质数。
请找出不超过1,0000,0000的所有满足这样的性质的正整数n的和:对于n的每个因子d,d+n/d是质数。
Problem 358
n位的「旋转数」有一个很有趣的性质:当它被乘以1, 2, 3, 4, ... n时,得到的积也具有同样的位数,每位数的排列顺序也和原来一样,只不过是位置旋转了一下!
最小的旋转数是6位数,即142857:
- 142857 × 1 = 142857
- 142857 × 2 = 285714
- 142857 × 3 = 428571
- 142857 × 4 = 571428
- 142857 × 5 = 714285
- 142857 × 6 = 857142
下一个更大的旋转数是0588235294117647,它有16位:
- 0588235294117647 × 1 = 0588235294117647
- 0588235294117647 × 2 = 1176470588235294
- 0588235294117647 × 3 = 1764705882352941
- ...
- 0588235294117647 × 16 = 9411764705882352
注意,对于旋转数,前置的0也在考虑之内。
已知,仅有一个旋转数,其开头11位数是00000000137,且末尾5位数是56789(即具有00000000137...56789的形式,中间有多少位数暂不清楚),请你找到这个数并求出它每位数的总和。
Problem 359
Hilbert的新无穷宾馆中有无穷位来宾(编号为1, 2, 3, ...)排着队等待进住。这栋宾馆有无穷层楼层(编号为1, 2, 3, ...),和无穷个房间(编号为1, 2, 3, ...)。
一开始这栋宾馆完全是空的,Hilbert给来宾的入住分配定下了一条规则:n号来宾入住编号最小的且满足以下任何一个条件的楼层的第一个空的房间:
- 这层楼没有人入住
- 这层楼已有人入住,假设上一个在这层楼入住的来宾编号为m,那么m + n是一个完全平方数
现在,1号来宾住1楼的1号房,因为1楼没人住。
2号来宾并不住1楼的2号房,因为1 + 2 = 3不是完全平方数。
2号来宾应该住2楼的1号房,因为2楼没人住。
3号来宾住1楼的2号房,因为1 + 3 = 4是完全平方数。
最终,每一位来宾都被分配到了一个房间。
设P(f, r)为n若n号来宾住f号楼层的r号房,为0若f号楼层的r号房没人住。如:
- P(1, 1) = 1
- P(1, 2) = 3
- P(2, 1) = 2
- P(10, 20) = 440
- P(25, 75) = 4863
- P(99, 100) = 19454
请求出所有P(f, r)的和,其中,正整数f和r满足f × r = 71328803586048。最后请给出你的计算结果的最后8位数。
Problem 360
假如三维空间里有两个点(x1,y1,z1)和(x2,y2,z2),那么它们之间的「曼哈顿距离」即为:
|x1-x2|+|y1-y2|+|z1-z2|
设C(r)为球心在原点O(0,0,0)且半径为r的球体,I(r)为C(r)表面上坐标值都为整数的点的集合,S(r)为I(r)中所有点分别与原点O之间的曼哈顿距离的和。
已知,S(45)=34518。请求出S(1010)的值。
Problem 361
一个叫做「Thue-Morse数列」的比特(只有0或1)序列{Tn}的定义如下:
- T0 = 0
- T2n = Tn
- T2n+1 = 1 - Tn
{Tn}的前几项如下:
01101001100101101001011001101001....
设{An}为转换为二进制数后在{Tn}中有出现过的十进制数的有序数列。
例如,十进制数18的二进制形式为10010,10010在{Tn}中出现过(T8到T12),因此18是{An}中的一项。
同样地,14可表示为1110,1110从来没在{Tn}中出现过,因此,14不属于{An}。
An的前几项如下:
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | … |
| An | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 9 | 10 | 11 | 12 | 13 | 18 | … |
已知A100 = 3251, A1000 = 80852364498。
请求出 的最后9位数。
的最后9位数。
Problem 362
数字54有7种因式分解的方法,因式分解中的因数都大于1:
54, 2×27, 3×18, 6×9, 3×3×6, 2×3×9, 2×3×3×3
若是要求所有因子都只能是无平方因子数,那么就只剩下两种分解式了:3×3×6和2×3×3×3。
令n 的因式分解中因数皆为大于1的无平方因子数的分解式个数为Fsf(n),故Fsf(54) = 2。
设S(n)为∑Fsf(k)的值,k = 2 至 n。
已知,S(100) = 193,请求出S(100,0000,0000)。
Problem 363
- 分别在线段P0P1, P1P2, P2P3上作三个点Q0,Q1, Q2,使得P0Q0/P0P1 = P1Q1/P1P2 = P2Q2/P2P3 = t,t ∈ [0,1]。
- 分别在线段Q0Q1, Q1Q2上作两个点R0, R1,使得Q0R0/Q0Q1 = Q1R1/Q1Q2 = t,t的值与上一步的相等。
- 在线段R0R1上作一点B,使得R0B/R0R1 = t,依然用上一次t的值。
- 点B随着点Q0在线段P0P1上移动所产生的移动轨迹即为我们要作的贝兹曲线。(t值保持不变)

你可以拖动右方面板中的点P0, P1, P2, P3来观察绿色的那条贝兹曲线的变化,也可以试试在线段P0P1上拖动Q0点。(译注:由于让浏览器支持Java控件太麻烦,于是我只提供了GIF图像。)
显然,通过这样的构造方法,贝兹曲线总是与线段P0P1相切于P0点,与线段P2P3相切于P3点。
由四个点P0=(1,0), P1=(1,v), P2=(v,1), P3=(0,1)可确定一条形状接近圆的四分之一的三次方贝兹曲线。v > 0,通过设置适当的v值,可令由线段OP0, OP3和贝兹曲线围成的区域的面积等于π/4(圆的四分之一的面积)。(译注:O为原点(0,0)。)
问:这条曲线的长与圆的四分之一的弧长相差百分之几呢?
即,假设贝兹曲线的长为L,那么求100×(L-π/2)/(π/2)。答案要精确到小数点后10位数。
Problem 364
有N张椅子被排成了一排,接着有N个人按照如下步骤陆续就坐:
- 若任一空椅子的旁边的椅子都没人坐,那么就坐这个椅子。
- 若没有这样的椅子,就找只有一个相邻椅子已有人就坐的椅子坐下。
- 假如还是不行,就随意找剩下的一个椅子来坐。
设T(N)为N人按如上规则坐上N张椅子的不同方案的总数。下图展示了T(4)=8的情况:
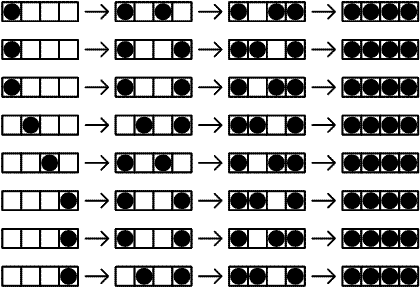
已知T(10) = 61632, T(1000) mod 1,0000,0007 = 47255094。请求出T(100,0000) mod 1,0000,0007的值。
Problem 365
二项式系数C(1018, 109)的位数超过了90亿(9 × 109)。
设M(n, k, m)为二项式系数C(n, k) mod m的值。
请求出∑M(1018, 109, p·q·r)的值,其中p, q, r三个质数满足1000 < p < q < r < 5000。
Problem 366
Anton和Bernhard两个人在一起玩一个游戏:
- 刚开始有一堆石子,共有n颗。
- 玩家轮流行动,第一回合行动的玩家可以移去其中任意正整数颗石子,但不能移去整一堆。
- 以后每一回合,玩家最多只能移去上一轮中对手移去的颗数的两倍的石子,且最少移去一颗石子。
- 先把石子移光的玩家胜出。
例如,当n = 5时:
- 若先手在第一回合移去超过1颗石子,则后手将可以在下一回合移去所有剩下的石子。
- 若先手在第一回合移去一颗石子,还剩下4颗,那么后手在下一回合也会移去一颗,然后剩下3颗。
- 在下一回合先手不能移去剩下的3颗石子,因果他最多可移去2x1=2颗石子,因此假设他只拿走1颗,留下2颗,那么后手就能移去剩下的两颗胜出。
于是n = 5对于先手来说是个必败的情况。
在某些必胜的情况中,先手在某回合中移去的石子的数量不止一种可能。如,当n = 17时,先手在某回合中可以移去1颗或4颗石子。
设M(n)为先手某回合中所能拿去的石子数量的最大值若他处在必胜的情况下,为0若他处于其它游戏状况下。
已知当n ≤ 100时,∑M(n)为728。
请求出当n ≤ 1018时∑M(n) mod 108的值。
Problem 367
bozo排序法,别以为它和效率更低的bogo排序法一样了,它首先判断输入序列是否已排序好,若不是,则随机交换两个项的位置,直到序列有序为止。
若以前4个自然数的全排列为输入序列,那么用Bogo排序法排序这4!个数所需的平均交换次数的期望值大概是24.75。当然,在已经排序好的情况下交换次数为0。
在这次的问题中,我们要用到的是bozo排序法的一个变种:
- 若序列不是有序的,那么就随机挑取3个项,并且像洗牌那样随机地改变他们的位置。
- 所有3! = 6个全排列出现的可能性相同。
- 有序的序列的交换次数为0。
已知,若输入序列为前4个自然数的全排列,那么用排序这4!个数所需的平均「洗牌」次数的期望值大概是27.5。
假如以前11个自然数的全排列为输入,那么以同样的方式排序这11!个数所需的「洗牌」次数的期望值大约是多少呢?
答案要精确到整数。
Problem 368
| 调和级数(harmonic series):1 | + |
|
+ |
|
+ |
|
+ ... 是一个发散的级数。 |
假如我们去掉其中分母包括数字9的项,那么它就会大大地收敛到大约是22.9206766193。这个被修改后的级数被称为Kempner级数。
现在我们再看看另一个被修改过的调和级数,这次要把调和级数中分母含有3个或更多的连续数字的项去除。可证明,调和级数的前1200项中只有20项会被去除,它们分别是:
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
. |
按上面方法修改过的级数也是收敛的。
请求出这个级数的收敛值,并把答案精确到小数点后10位数。
Problem 369
若用一副标准的52张一副的扑克,一组4张既没有对子也没有相同花色的纸牌被称为Badugi(译注:一种特殊的散牌)。
设f(n)为从一副52张的扑克里选取n张纸牌,且纸牌中含有Badugi的方式种数。
已知,若选取5张纸牌,则2598960种选择方式里共有514800种含有Badugi,因此f(5) = 514800。
请求出∑f(n)在4 ≤ n ≤ 13范围内的值。
Problem 370
现定义一个「几何三角形」为整数边长的三角形,且三条边的长度a ≤ b ≤ c符合b2 = a · c。
有很多像这样的几何三角形,如边长分别为a = 144, b = 156, c = 169。
已知周长不超过106的几何三角形共有861805个。
问:周长不超过2.5×1013的几何三角形有多少个?
Problem 371
美国奥勒岗州的车牌号码是由三个大写字母后接三位数字组成的(每个数字的范围是0-9,每个字母的范围是A-Z)。
Seth每次驾车上班时都会玩下面这个游戏:
假如他一路上看见两个车牌的号码的数字加起来恰好是1000的话他就赢了。
如,看到MIC-012和HAN-988就算他赢了,或者RYU-500和SET-500,等等。(只要是同一天看见的就行。)
请求出他要获胜时看到的车牌号的个数的期望值。答案要精确到小数点后8位数。
注:假设看到的每个车牌号的三位数字出现的概率对于每三个字母都一样。
Problem 372
设R(M, N)为满足M < x ≤ N, M < y ≤ N且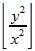 是奇数的网格点(x, y)的个数。
是奇数的网格点(x, y)的个数。
已知R(0, 100) = 3019, R(100, 10000) = 29750422。求R(2×106, 109)。
提醒:⌊x⌋表示向下取整。