圓的角度為360度，這是一個顯而易見的事實，對嗎？

錯了。大部分人並不知道為什麼圓有360度。我們隻是把它當作一個神奇的數字，也就是“圓的大小”來記憶，這導致我們以後在物理或數學的學習中，對所謂的“弧度”充滿困惑。

專家們說“弧度讓數學更容易！”，但是從來不解釋其中的原因（其中涉及到的泰勒級數並不簡單）。今天讓我們揭開弧度的真實一面，以一種更直觀化的方法來理解它為什麼讓數學更簡單。

4.1 角度是從哪裏來的呢？

在數字與語言發明之前我們有星星。古代文明利用天文學來標記季節，預言未來，安慰神靈（用人獻祭時要保持准時）。

這跟角有什麼關係呢？呃，小子，猜猜這個：圓有360度，而一年有365天，這個不奇怪嗎？在一年之中，星座正好在天空中盤旋，這個不也是很奇怪嗎？

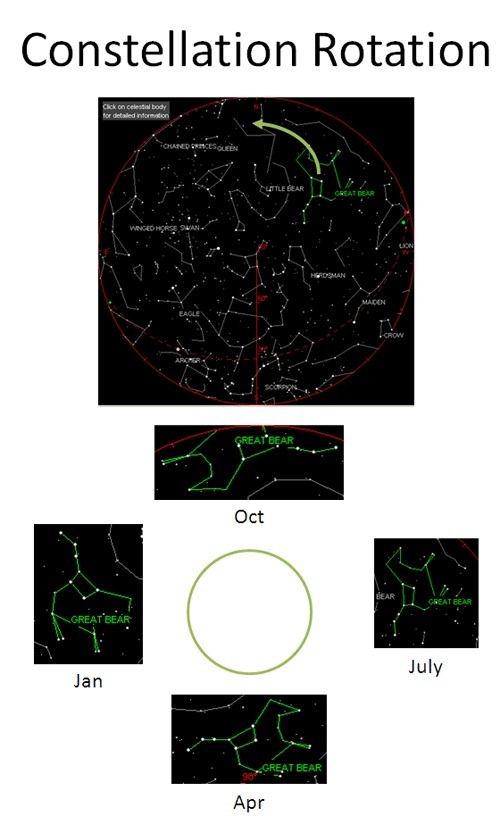
你如果是個不懂航海的人的話，肯定不能像海盜那樣通過夜空來判斷季節。這是2008年，在紐約看大北鬥星座（大熊星座）的星圖（如圖）。

星座每天都要在繞圈。如果你每天都在同一時間（半夜）觀察的話，一年之內它們將畫出一個完整的圈。這就是角度產生的理論：

• 人類註意到星座每年都劃一個完整的圈
• 每天，它們都移動一點（“一度”）
• 因為一年大概有360天，所以一個圓也就有360度。

但是，但是……為什麼不是365度呢？

別太苛求了：它們有日規儀，但是他們不像我們一樣精確的知道一年有365.242199天。

360已經是一個足夠應付那時的需要了。它非常完美的契合了巴比倫的60進制計數法，而且可以很好的被整除（被2，3，4，6，10，12，15，30，45，90，…………整除，你懂了吧）。

4.2 基於太陽的數學看起來非常合理

地球正好沒被選中：一年中有360天很完美。但是這個好像是完全任意的：如果在火星上的話，一火星年較長（火星日也較長，但是你明白其中的要點就好了），所以圓大概有680度。歐洲有些地區使用另一種歷法，一個圓大概被分成了400份。

許多解釋到這裏就結束了，“圓的角度是任意的，但是我們總需要選一個數字來表示吧”，而不是“我們要明白角度的整個假設基礎就必須追溯到以前”。

4.3 弧度有規則，角度則是在胡扯

一個角度是一個數字I，觀察者，需要傾斜自己的頭來看到你，那個運動者。這樣有些自私，你不這樣認為嗎？

你：嗨，比爾，你走了多遠呢？

比爾：呃，我的速度不錯，大概走了6到7英裏吧—

你：閉嘴。為了看到你我的頭運動了多遠？

比爾：什麼？

你：我簡單告訴你。我在跑道的中央。你在周圍跑。我的頭轉動了多少？

比爾：你個混蛋。

很自私，是吧？這就是我們怎麼用數學的！我們寫下方程式“嘿，我的頭轉動了多少才看見那個星球/擺鐘/輪胎移動？”。我敢說你肯定從來沒關心過擺鐘的感受。

你不認為物理方程式無論是對運動者還是對觀察者都應該保持簡單嗎？

4.4 弧度：不再自私的選擇

許多物理問題（包括大部分生活）都需要你選定一個參考系，然後以一個第三者的角度盡心觀察。與其關心我們的頭轉過了多少，不如考慮一下別人走了多遠。

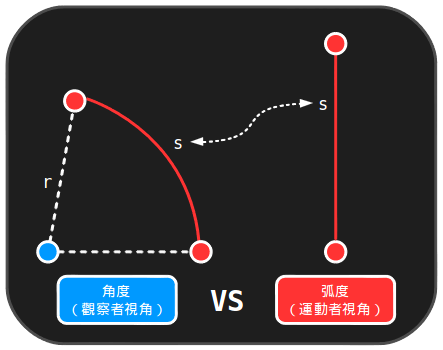
角度是通過測量我們的頭轉過了多少而確定。弧度則是通過測量走過的距離來確定。

但是絕對距離並沒有什麼用，因為跑道不同，同樣走十英裏也是不同的。所以我們除以半徑來獲得一個更一般化的角度：

弧度＝走過的距離/半徑

你經常見到的形式是θ＝s/r，或者是弧度中的圓心角＝弧長除以半徑。

一個圓有360度或者是2π弧度——繞圓完整一圈的的距離2πr/r。所以一弧度大概是360/2π或者57.3度。

不過不要像我一樣，又在“記憶一個神奇的單位量，57.3度是這麼怪”。因為你還是在以一個自私的角度去考慮它。

移動一弧度（單位）是一個很正常的距離。換言之，“幹凈的90度角”意味著運動了“非常不好看的π/2個單位”。想一想這個——“嘿，比爾，你能給我跑90度嗎？那是什麼啊？哦，對了，在你看來那就是距離我π/2英裏遠的地方。”兩種方法都很生分。

弧度是以一種換位的方式來做數學——不再是以觀察者的頭轉動了多少而是以運動者的角度去考慮問題的方法。

嚴格說來，弧度就是一個比例（兩個長度之比），沒有範圍限制。通俗地講，我們不是數學機器，這樣可以幫助我們認為弧度是走了“一單位圓的距離”。

4.5 使用弧度

我還是習慣使用弧度來思考。但是我們經常會遇到“運動的距離”這一概念：

• 我們測量一個轉動速度時使用“每分鐘的轉數”而不是“每秒轉過的角度”。這是以運動者的參考點（“走了多少圈呢”）來考慮，而不再是考慮任意的角度測量。
• 人造衛星繞地球轉動時，我們能理解“英裏每小時”這個速度，但是不能理解“角度每小時”這個速度。現在除以距離便得到人造衛星弧度每小時的速度大小。
• 正弦函數，非常神奇的一個函數，可以利用弧度來定義：$\sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots$

這個公式隻有當x是弧度的時候才成立！為什麼呢？正弦函數的基礎就是移動的距離，而不是以頭的轉動來衡量。以後我們再詳細討論這個問題。

4.6 弧度示例1：公車的輪胎

讓我們舉一個現實生活中的例子：你有一個擁有輪胎半徑為兩米的公車（這是怪物公車）。我說公車輪胎轉得有多塊，你說從車走得有多快。准備好了嗎？

“輪胎每秒轉動2000度”，你會這樣想：

OK，輪胎每秒轉2000度。這就是說2000/360，為5又5/9圈每秒。圓周＝2πr，所以它轉動，呃，2乘以3.14乘以5又5/9圈……我的計算器在哪裏呢？

“輪胎每秒轉動11弧度”，你會這樣考慮：

弧度就是沿著單位圓走過的距離——我們隻需乘以真實的半徑就可以得到我們走過的距離。11乘以2等於22米每秒。下一個問題。

哇哦！沒有複雜的方程式，沒有麻煩的π——隻是簡單的相乘然後就能把轉動的速度轉變為直線運動的速度。一切隻是因為以弧度來表示。

反過來做也一樣容易。假設我們在高速公路（60英裏每小時）上以90英尺每秒的速度行使，輪胎為24英寸寬（半徑為一英尺），我們的輪胎轉得有多塊呢？

好的，90英尺每秒/1英尺的半徑＝90弧度每秒。

相當簡單。我甚至認為饒舌歌手也是因為這個原因所以才唱“24 rims”。

4.7 弧度示例2：sin(x)

讓我們舉個更好的例子。計算涉及到許多東西，其中就有當數字變得很大或者很小的時候會怎麼樣。

選擇一個度數(x)，然後把Sin(x)輸入你的計算機：

當你取的x很小時，比如說0.01，Sin(x)也會變得很小。而Sin(x)/x的值大概為0.17——這意味著什麼呢？更進一步，乘以或除以一個角度意味著什麼呢？你能把角度平方或者立方嗎？

弧度就是救世主！它與走過的距離有關（它不止是一個比例！），我們可以這樣解釋這個方程組：

• x是沿著一個圓走了多遠
• sin(x)是你在這個圓上有多高

那麼sin(x)/x就是你的高度與你所走過的距離的比：也就是你在向上的方向上你所具有的能量。如果你垂直移動，那麼比例就是100%，水平移動就是0%。

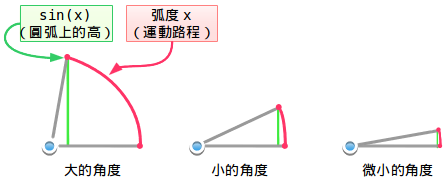
如果我們移動一個很小的角度，比如說從0度到1度，那麼它基本上就是垂直的移動上去的。如果是更小的角度，比如說是從0度到0.00001度，那麼它真的就是垂直移動上去的。移動的距離與它的高度近乎相等。

隨著x的縮小，比例逐漸接近100%——更加接近於垂直移動。弧度幫助我們直觀化的理解為什麼當x足夠小的時候sin(x)/x接近於1.我們隻是在垂直方向輕輕向上推了一點而已。而且這也正好揭示了為什麼隻有x取較小的值的時候，sin(x)約等於x。

記住，這些結果隻在以弧度為測量單位時才成立。如果是以角度為單位，你就是在比較你的高度與你的頭轉過的角度，這個比例變化的賊快。

4.8 那麼有很麼意義呢？

角度有著它的地位：在我們的生活中，我們處在自己的焦點中，並且觀察著周圍的事物如何影響我們。我該把我的望遠鏡傾斜多少度，我的滑雪板應該轉過多少度，或者是方向盤應該轉過多少度。

我們作為一個觀察著描述其他運動的物體是一個自然而然的事。弧度是關於運動物體的，而不是關於我們的。我花了很長時間才意識到這一點：

• 角度是任意的，因為它是基於太陽運動的（365天~360度），但是因為是基於觀察者的角度，所以比較落後。
• 因為弧度是以運動者的角度來定義的，所以公式簡單明了。把轉動速度變為線性速度相當簡單，而且sin(x)/x之類的也有意義。

即使是角也可以從不止一個角度來理解，而理解了弧度可以讓數學與物理更加直觀。希望你能享受到快樂的數學。