理解指數

我們知道指數就是重復的乘法。這是個很好的介紹，但是它不能解釋3^1.5 ，同樣也無法讓人理解0⁰ 。你怎麼能說清楚讓0乘以自己0次然後就得到1了。

你不能，當你把指數解釋為重復的乘法時你就沒法解釋。今天我們就要把這個模型做一次升級。

 

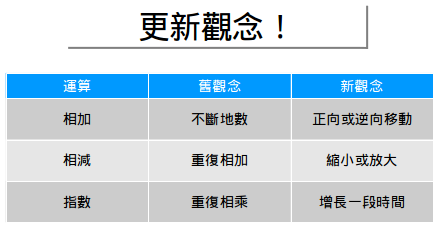
10.1 把算術看作是變換

讓我們再退回去看看——我們是怎麼學習算術的？我們知道數字是指一些東西的個數（手指），加法就是把這些個數組合起來（3+4＝7），而乘法就是重復的加法（2×3＝2+2+2＝6）。

這種解釋在約整數身上很正確。但是用在像-1與根號2這類數字上就比較奇怪了。為什麼呢？

我們的模型並不完整。數字不隻是個數；更好的觀點是吧它們當作直線上的一點。這個點可以是負的（-1），也可以是其他數（根號2），或者是在另一個維度（i）。

算術就是對數進行變化的一種一般方法。加法就是沿著數軸進行移動（+3就是向右移動三個單位），乘法就是按比例縮放（×3就是放大三倍）。

那麼指數是指什麼呢？

10.2 進入“創世界”（Expand-O-Tron）

先讓我介紹一下創世界3000 。

是的，這台設備看起來像是一台劣質的微波爐——但是它並不是用來加熱食物而是用來使數字增長的。輸入一個數字，它就產生一個新的數。以下是整個過程：

1. 以1.0開始
2. 設置1秒後的增長倍數（2×，3×，10.3×）
3. 設置增長的時長
4. 按下開始鍵

太上老君如律令，快變！鈴聲響起，然後我們就得到了新鮮閃耀的數字。假設我們想把1變為9：

1. 在“創世界”中輸入1.0
2. 設置增長倍數為“3×”，時間為2秒。
3. 按下開始鍵

我們按下開始後，數字就開始發生變化：我們看到1.0，1.1，1.2，……就在第一秒剛剛結束的時候，我們得到了3.0.然後繼續增長：3.1，3.5，4.0，6.0，7.5……然後就在第二秒結束的時候我們得到了9.0 。我們看到了閃亮的新數字。

從數學角度來講，“創世界”（指數函數）是在做：

原始數字·增長率^時間 ＝新數字

或者是：

增長率^時間 ＝新數字/原始數字

舉例來說，3² ＝9/1 。底就是每單位增長的量（3×），而指數就是增長的時間（2）。2ⁿ 這樣的公式就是說“使用’創世界‘以2倍的增長率增長n秒”。

記住，在“創世界”中我們總是以1開始，然後來觀察每單位的變化。如果我們想看看以3開始會發生什麼，我們隻需放大結果就可以了，舉例如下：

• “以1開始，增長3秒”就是說1·2³ ＝1·2·2·2＝8
• “以3開始，增長3秒”就是說3·2³ ＝3·2·2·2＝24

每當你看到一個普通的指數時（比如說2³），那就是暗示它是以1開始，以2倍的增長率增長3秒所達到的值。

10.3 理解指數縮放因子

當我們做乘法運算時，我們可以表明最終的縮放因子。希望它有八倍大，乘以8就搞定了。

指數有些過於……苛求了：

你：我想增長一個數字。

創世界：好的，把它放進來吧。

你：它會有多大呢？

創世界：老兄，我現在不知道啊，讓我們走著瞧吧

你：走著瞧？我還以為你知道呢……

創世界：噓！！！它在增長，在增長！

你：……

創世界：好了，看看我的傑作吧！

你：我現在可以走了嗎？

“創世界”是間接的。看看它，你都不知道它會做出什麼：3¹⁰ 最後是多少？你對此有什麼感覺？不是直接完成比例系數，指數希望你能去感覺，去重生，甚至是去聞聞增長的進程。不管最後是什麼那都是你的比例系數。

聽起來像是繞圈子。你知道為什麼嗎？自然界中的許多事物都不知道將在何時終止！

你認為細菌知道每24小時翻一倍嗎？肯定不知道——它隻知道儘快吃掉你忘在冰箱裏的麵包，然後儘快的讓菌斑快速生長起來（當然，這純屬假設）。為了預測這種行為，我們輸入它們生長的速度，還有它們生長的時間，然後得出它們最後的總量。

肯定能得到一個答案——指數就是一種“給定初始條件，開始改變，然後看它結束時的量”的說法。“創世界”（我們的計算器）可以完成這種計算。總之總得有人完成這些計算。

10.4 理解分數冪

讓我們看看“創世界”能否幫助我們理解指數。首先：2^1.5 是什麼意思呢？

當我們把指數看作連續相乘時，這個問題就讓我們很疑惑。但是“創世界”讓它變得簡單：1.5隻是在這台機器中需要的時間罷了。

• 2¹ 就是說在這台機子中1秒的時間（增長了2倍）
• 2² 就是說在這台機子中2秒的時間（增長了4倍）

所以2^1.5 就是在這台機器匯總1.5秒，最後就是增長了2到4倍之間。而那個“重復計數”的想法則把我們困在了整數中。

10.5 指數相乘

如果是讓兩次增長緊接著發生會怎樣呢？就是說我們先用上這台機器2秒，然後緊接著又使用3秒：

x² ·x³ ＝？

想想你家用的微波爐——這不就是連續使用5秒嗎？確實是這樣。這樣底保持不變，我們就可以把時間相加：

x^y ·x^z ＝x^y+z

再一次的，“創世界”給了我們一個縮放因子來改變數字。為了得到兩次連續使用的總效果，我們隻需把時間相加就可以了。

10.6 平方根

讓我們繼續前進。假設我們有冪為a，增長3秒：

a³

不算太壞。如果增長一半的時間會是什麼結果呢？就是1.5秒：

a^1.5

如果我們把這個過程做上兩次會是什麼結果呢？

a^1.5 ·a^1.5 ＝a³

換言之就是：部分增長×部分增長＝總增長。

看看這個方程，我們看到“部分增長”就是總增長的平方根！如果我們把時間除以二就得到了它的平方根。如果我們除以3呢？

a¹ ·a¹ ·a¹ ＝a³

或者：部分增長×部分增長×部分增長＝總增長

我們得到了立方根！對我來說，這就是指數相除就可以得到根的直觀化理由：我們把時間分成了相等的部分，所以每一個“部分增長”的效果都一樣。如果是三個相同的效果相乘，那就是說它們都是立方根。

10.7 負指數

我們繼續深入——負指數是什麼意思呢？“負秒”就是讓時間倒流！如果時間倒流的話，原數值也應該隨之縮小：

2^-1 ＝1/2¹

這就是說“1秒以前，我們有現在值的1/2”。事實上，這隻是任何指數圖像的一部分而已，比如說2^x ：

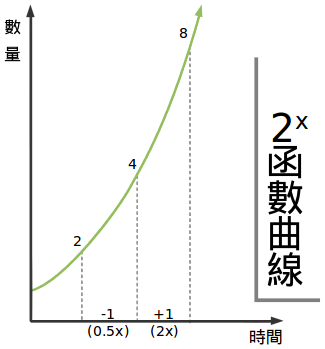
任選一個點，比如說3.5秒（2^3.5 ＝11.3）。向前一秒現在的數值就會翻倍（2^4.5 ＝22.5）。向後一秒我們就得到了現在數值的一半（2^2.5 ＝5.65）。

這對任何數字都適用！即使是在我們的雙倍增長曲線的一百萬的那個點處，我們也隻不過是在它500000秒之前而已。

10.8 指數為零

讓我們再看看比較麻煩的一部分：3⁰ 意味著什麼呢？我們給機器設置了3倍的增長率，然後使用了0秒。0秒就意味著我們沒有使用這台機器！

我們新的值與舊的值完全一樣（新＝舊），所以比例系數就是1。0指數就是說沒有變化。比例系數始終為1。

10.9 如果以0為底

我們如何解釋0^x ？因為增長率為“0倍”——一秒之後，“創世界”就會把最初始的值給抹為0。但是如果我們在1秒後抹掉了數值，那麼以後的任何時間都為0：

0^1/n =0¹ 的n次根＝0的n次根＝0

無論我們列舉的指數有多小，它們都是0的某次根而已。

10.10 0的0次指數

最後，是令人畏懼的0⁰ 。它的含義是什麼呢？讓“創世界”來幫助我們吧：

0⁰ 就是說以0倍增長0秒！

即使我們打算抹掉這個數字，但是我們根本沒有使用這台機器。沒有使用就是新的＝舊的，而縮放系數是1。所以0⁰ ＝1·0⁰ ＝1·1＝1——它並沒有改變什麼，謎題解開了！

（對於數學家來說：定義0⁰ ＝1可以讓很多理論很自然的建立起來。在現實生活中，0⁰ 要根據具體情況來判斷（是連續的還是分立的）。類比微波爐並不嚴謹：但是它幫助我們理解0⁰ ＝1為什麼合理，而“重復相乘”做不到這一點。）

10.11 高級：重復指數（a到b然後再到c）

重復指數需要一些技巧。下面該式表達了什麼呢？

（2^a ）^b

它表示“重復相乘，再重復相乘”——換言之就是“指數一次後再指數一次”，把它分解開來：

（2³ ）⁴

• 首先，我希望先翻倍增長3秒（2³）
• 然後，不管新數字是多少（8倍），我希望它按照那個倍數增長4秒（8⁴）

第一個指數（³）就是取“2”然後自乘3次。第二個指數（⁴）就是把之前的數字自乘4次。

（2³ ）⁴ ＝2³ ×2³×2³×2³ ＝2^3+3+3+3 ＝ 2¹²

重復計數幫助我們明白現在的處境。但是當我們繼續使用“創世界”進行類比後：我們第一次增長3秒，然後第二次再增長4秒。“創世界”同樣可以使用分數：

（2^3.1 )^4.2

這就是說“先增長3.1秒，然後使用新數值增長4.2秒”。最後我們可以把它們合到一起（3.1×4.2）：

（a^b ）^c ＝a^b·c ＝(a^c )^b

重復指數有些奇怪，所以我們還是舉些例子：

• （2¹ ）^x 就是指“以2倍增長1秒，然後再按這種增長倍數增長x秒”。
• 7＝（7^0.5 ）² 就是說我們可以直接到達7，也可以，我們可以先用一半的時間增長到根號7，然後再把這個過程進行2秒，就得到了7。

我們就像孩子一樣學習7×3＝3×7。

10.12 高級：為增長者重寫指數

“創世界”有點怪：數字隻要一進去就開始變化，但是我們想在每一秒結束時指定不同的增長倍率。

假設我們想在第一秒結束時有2倍的增長。但是我們怎麼知道開始時的增長率是多少呢？0.5秒的時候應該有多少呢？肯定不是完整值，否則我們就會計算出到超過實際的復利。

這就是關鍵點：寫作2^x 的增長曲線是以觀察者的角度來看的，而不是增長者。

“2”是根據每個時間間隔後的結果來決定的，我們倒回去創造了這個指數（哦，這就像你在以2^x 在增長一樣）。這樣做會讓我們看起來很舒服，但是對增長數量來說可就不好了——細菌，放射性元素還有金錢可不會對准我們設置的間隔！

自然不會這樣，這些傢伙隻知道它們現在的，當下的增長率，它們不會想去如何對齊我們設置的邊界。這就像理解角度與弧度一樣——弧度很“自然”因為它是從運動者的角度去考察的。

為了以增長者的角度考察這個問題，我們引入神奇的數字e。這其中有太多東西可講，但是我們在這裏隻是把“基於觀察者”的方程比如說2^x轉化為“基於增長者”的方程：

2^x ＝（e^ln（2））^x ＝e^ln（2）x

在這個例子中，ln（2）＝0.693＝69.3%就是當下的增長率，當你問“創世界”每個週期2結束時2倍的增長是多少時，它就會回答以69.3%增長。

還有更多的細節有待挖掘，但是記住：

• 當下的增長率是由細菌自己控制的。
• 每個時間間隔的總體增長率是由觀察者測定的

從本質上說，任何指數曲線都可以化為e^x 的某個比例的版本：

a^x ＝（e^ln（a））^x ＝e^ln（a）x

任何指數都是e的一個變化，就像任何一個數都是1的倍數一樣。

10.13 為什麼要進行類比？

真的有“創世界”嗎？所有的數字真的集中在一條直線上嗎？不實的——它們是觀察世界的一種方法。

“創世界”去除了對待2^1.5 甚至是0⁰ 次時的一些問題。這樣一來從計算尺到歐拉公式都可以按照增長這個主題來看待——即使是像iⁱ 這樣的野獸也可以被馴服。

不要讓你的朋友們還在認為指數僅僅是重復相乘了。希望你能享受到快樂的數學。