歐拉公式

歐拉公式看起來完全讓人摸不著頭腦：

e^ix ＝cos(x)+isin(x)

這就是說：

e^iπ=cos(π)+isin(π)=-1+i(0)=-1

這個結果是如此的不真實，所以我打算再把它重寫一次：

e^iπ ＝－1

這個方程式把虛指數與正餘弦函數聯繫起來。它是怎麼把一個像Pi這樣的無限不循環小數這麼簡單的就變為-1了呢？這能有一個直觀化的解釋嗎？

這裡不得不提到19世紀的數學家Benjamin Peirce：「這絕對是個悖論；我們不可能理解它，我們甚至都不知道它是什麼意思，但是我們既然證明了它，那麼我們就知道它是真的。」

這種態度讓我大為火光。我們應該直接舉手投降，然後死記硬背嗎？不！

歐拉公式描述了沿著圓運動的兩種方式。僅僅是這樣嗎？最有魅力的公式之一就是轉圈圈？沒錯——今天我們就來看看這是為什麼。

11.1 理解cos(x)+isin(x)

方程式符號承載的東西太多了。有時候它隻是表示「把一個東西變為另一個東西」（比如說x＝3）而已。而另一些時候它隻是表示「描述同一事物的兩種不同方法」（比如說根號負一等於i）而已。

歐拉公式就是在描述兩種描述統一現象的等價方法：轉圈圈。為了達到我們的目的，假設你前進了x弧度：

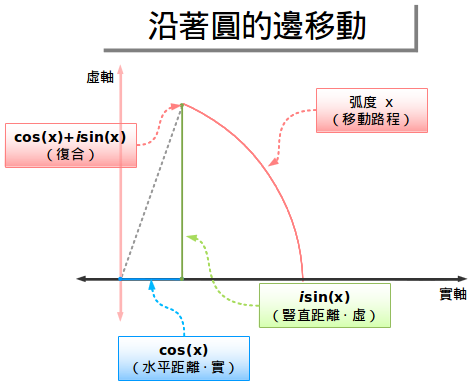
• cos(x)就是x軸的座標（水平距離）
• sin(y)就是y軸的座標（豎直距離）

cos(x)+isin(x)是一種很聰明的辦法，它把兩個座標整合到了一個複數中。「複數有兩個維度」的類比幫助我們很好的把這些即時作了二維平面上的一個點。記得我們在第一章給圓下的定義嗎？現在我們來加入一些新的東西。

當我們寫下x＝π（在這個例子中表示讓x的值為π）時，就是說我們沿著單位圓運動。因為圓周長是2π，所以我們走了一半的距離。

從1開始前進π弧度，我們的起始點在單位圓上，終點就是-1。沒有虛部（y軸座標），因為-1就在實數軸上。如果我們是令x＝-π，沿順時針方向前進的話，我們得到相同的結果：-1。

很酷吧。所以歐拉公式就是說e^ix 跟(cos(x)+isin(x))表示相同的沿著單位圓進行的運動過程。現在我們來看看e是怎麼做到這一點的。

11.2 什麼是虛部增長呢？

用x、y座標表示虛數需要一些技巧，但是是完全可行的。但是虛指數到底是什麼意思呢？

讓我們再回想一下那台「創世界」機器。3⁴ 這樣的東西表示「以3倍的增長率增長4秒」。以增長者的角度來看：

3⁴ ＝（e^ln（3））⁴＝e^ln(3)‧4

增長者隻知道它現在的增長率(ln(3)，所有的複合增長完成後就變為3)，它想讓我們把增長率擴大到4倍。那麼乘以4就可以了：

e^ln(3)‧4 ＝81。

現在，我想問問為什麼可以擴大四倍呢？那是因為乘以4（一個實數）就表示擴大四倍。但是虛數就不一樣了：當乘以一個虛數後，其實是把結果旋轉了。

11.3 把增長旋轉一下

通常的增長就是推動一個數字沿著一個固定的方向前進：2×3就是把2沿著原始方向，把它推到3倍大（6）。

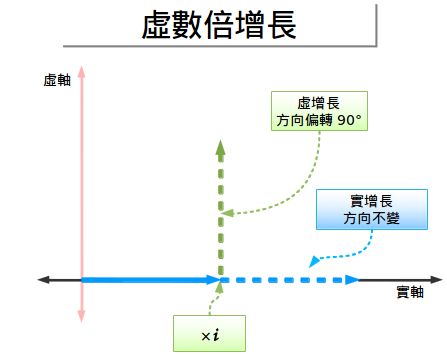
但是一個虛數倍的增長會把你的「增長」旋轉90度到虛軸上！簡單來說就是一個與原來方向正交的推動並不會讓你的增長速度變快或變慢——它是要把你旋轉一下！任何實數乘以i並不改變大小，隻會改變方向。

直觀的來看，當我們在討論虛增長時，實際上就是在說：

虛增長：當我增長的時候，不要把我推向前或向後，而是要旋轉我。

一個常數旋轉並不會改變你的大小——你隻是會轉圈圈而已。

11.4 但是我們不是應該越轉越快嗎？

不是的。我來跟你解釋一下：常規的增長讓你在原來方向上前進或後退。所以你從1開始，到2，4，8，16，你每次都是乘以一個2，然後你依然是個實數。

但是純粹的虛增長隻是讓你旋轉。讓我們假定你在i方向的增長率是100%：你保持一個恆定的推動，所以最後的效果也就是旋轉而已。

1秒之後你在90度方向（i），2秒後，你在180度方向（i²＝-1），這樣不斷進行。虛增長不進行復合！如果你的增長率是一個較大的虛數（2i），你可以認為這個增長需要兩倍長的時間（還記得e把時間與增長率合併到一起嗎？）。但是它還是在一個垂直的方向進行推動，而這不會改變你的速度。

現在，如果你的增長率是個複數（a+bi），那麼實數部分就跟常規增長一樣表示你是增長還是縮少，而虛數部分表示將把你旋轉。但是歐拉公式（正如它的形式一樣）是關於純粹的虛增長（e^ix）的。我們接下來的討論會更複雜一些。

11.5 追根溯源

讓我們湊近點看看。回憶一下關於e的這個定義：

$e=\lim_{n\to\infty}\Big(1+\frac{100\%}{n}\Big)^n$

　　1/n表示在我們的週期內賺到的利潤。我們假設利潤是實的——但是如果它是虛的呢？

$e = \lim_{n\to\infty}\Big(1+\frac{100\%\cdot i}{n}\Big)^n$

現在我們的利潤被推向了90度方向，但是這不影響我們的長度。（這是一個比較難理解的概念，因為這就像我們在一個比較長的斜邊下構造一個三角形。我們在處理一個極限；斜邊有一個在我們誤差範圍內難以發現的增加。我們需要微積分來幫我們弄清楚，但是這個還是改日再談吧）。

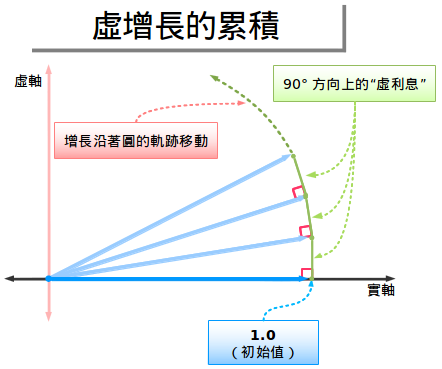
我們每次把i單位的增長應用到無窮小量上。每一次應用都是輕輕把它推向90度方向。沒有所謂的「越來越快」的旋轉，因為它與增長方向始終保持垂直，它隻是推向一個新的方向而已（+1角度而已）。

所以我們發現了另一種表示圓的方法！

圓周運動：始終沿著90度的方向進行旋轉（虛增長率）

那麼，歐拉公示就是在說「指數的虛增長最後就是一個圓的軌跡」。而這個軌跡跟用正餘弦函數表示的虛數畫出來的軌跡一樣。在這裡用「指數」可能有些不 恰當，因為我們沿著一個圓始終做著勻速運動（最好還是稱為「連續改變」）。但是我們現在主要面對的是增長就是一個復合的，累積的增長。

11.6 一些例子

你現在可能不相信我。以下是一些幫助你直觀化思考的示例。

示例：eⁱ

x在哪裡呢？哈哈，它就是1.直觀的來看，不需要用計算器我們就知道這是在說「沿著單位圓前進1弧度」：

eⁱ ＝cos(1)+isin(1)=0.5403+0.8415i

不是一個簡潔的數字，但是依然有效。輸入這些的時候記得把你的計算器調到弧度模式。

示例：3ⁱ

這就需要一些技巧了——這不是我們通常見到的形式。但是記住，3ⁱ ＝1‧3ⁱ ——真正的問題就是「我們怎麼把1做變換」呢？

我們希望有一個最後增長率為3倍或者說即時增長率為ln(3)的增長，但是，i把ln(3)變成了ln(3)‧i：

3ⁱ ＝(e^ln(3))ⁱ  = e^ln(3)‧i

我們本來以為我們隻是轉換一個ln(3)就夠了（因為e是2.718，所以這個比100%要快一些）。但是，哦，i讓我們團團轉：現在我們把它轉換成了虛增長，這就意味著我們在旋轉。如果i是一個常規數字比如說是4，我們就會得到一個4倍快的增長。現在我們的增長速度是ln(3)，不過是在一旁增 長。

我們應該能夠想到一個單位圓上的複數——不會改變我們的大小。解這個方程：

3ⁱ ＝e^ln(3)‧i ＝cos(ln(3))+isin(ln(3))=0.4548+0.8906i

示例：iⁱ

在之前見到這個傢伙會直接把我嚇跑，很有可能還帶著淚水。但是現在我們可以把它做一些變換：iⁱ ＝1‧iⁱ 。我們從1開始變化。就像解決3ⁱ 那樣，以i為底時現在的即時增長率是多少呢？

呃，通常我們會用ln(x)來得到在最終達到x的即時增長率。但是對於虛增長率？我們需要做些改變。

為了從1變到i，我們需要旋轉。轉多塊呢？好吧，我們需要在一單位時間內轉過90度角(Pi/2弧度)。所以我們的增長率就是Pi‧i/2（記住我們是要旋轉所以必須乘以一個虛增長率）。

這樣就可以說得通了：在一單位時間內，把1變到i，我們應該旋轉Pi/2弧度（90度角）。

這個解釋了底，但是對於指數呢？

另一個i告訴我們改變增長率（是的，我們應該花多長時間轉動就可以結束了），乘以i表示以Pi‧i/2的速度進行旋轉：

Pi‧i‧i/2＝Pi/2‧(-1)＝－Pi/2

i被消去了，增長率又變為了實數！我們把增長率轉到了一個相反的方向。這意味著我們在縮小——我們應該能夠想到iⁱ 就是讓事物變小。事實確實如此（在Google中搜索「i^i」來利用它的計算功能）

先喘口氣：你應該可以直觀化的瞭解到，虛數底與虛指數的行為是怎樣的。

示例：（iⁱ )ⁱ

想要更多？如果你堅持的話，首先我們知道括號內的增長率等於多少：

iⁱ ＝（e^Pi‧i/2）ⁱ ＝e^-Pi/2

我們得到了一個Pi/2的負增長（縮小）。現在我們用i來修改一下它：

(iⁱ )ⁱ =(e^-Pi/2)ⁱ =e^-Pi‧i/2

我們得到了一個負旋轉！我們每單位時間將要以Pi/2的速度進行旋轉。轉多長時間呢？其中暗示了1個單位時間；一個單位時間的旋轉就是-i：

iⁱ =0.2078……

(iⁱ)ⁱ=-i

而且，看看整個過程，如果我們給它平方一下的話：

((iⁱ )ⁱ )² =-1

這就好比是兩倍的旋轉：2是一個實數，所以它讓我們的旋轉翻倍到-180度。或者也可說它做了兩次-90度的旋轉。

最後得瑟一下，它們確實都是些奇怪的指數，但是通過類比我們可以很輕鬆的把它們搞定。

11.7 混合增長

我們可以既有實數增長也有虛數增長：實數增長改變大小，虛數增長進行旋轉：

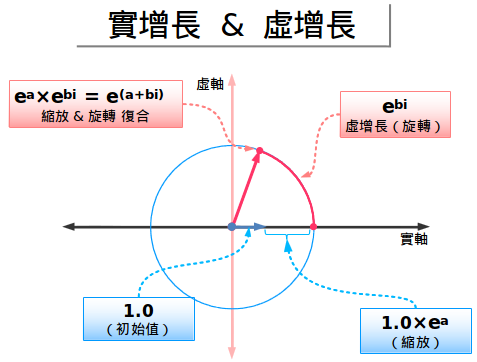
一個複數增長率（a+bi）就是混合了實數增長與虛數增長。實數部分就表示「每秒增長100%」而虛數增長就是「旋轉b秒」。記住，虛數並不能把不同的方向進行復合，所以它隻是線性相加。

根據這個想法，我們可以把任何點用不同大小的圓（a+bi）表示出來！半徑就是e^a 而角度由e^ib 決定。這就像把數字放到「創世界」中兩次：一次你讓它的大小發生變化（一秒），另一次就是讓它的角度旋轉（b秒）。或者你可以先旋轉再增長！

我們想知道得到6+8i的最終倍數所需要的增長數。這就是在問一個複數的自然對數：我們如何把e變為6+8i？

• 半徑：我們需要一個多大的圓？大小是10.這就意味著需要花ln(10)=2.3秒的時間來達到這個數值
• 旋轉的角度：那個點的角度是多少？我們可以使用反三角函數來計算：arc tan(8/6)=53度＝0.93弧度。
• 組合結果：ln(6+8i)=2.3+0.93i

11.8 為什麼真很有用？

最起碼的，歐拉公式給了我們一個另一種方法來描述沿著圓的運動。當然我們也可以用正餘弦函數來表示——為什麼如此特別呢？

這隻是角度不同而已。正餘弦函數運動就是在水平座標和垂直座標中運動的點而已。

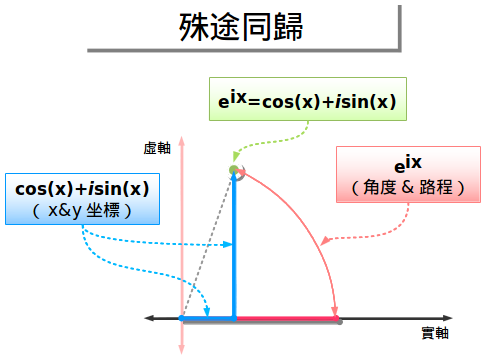
歐拉公式使用極座標——你的角度與距離多少？再一次的，這是兩種描述運動的方法而已：

• 網格系統：向東3個單位，向北4個單位
• 極座標：在71.56角度上移動5個單位

這取決於是哪種問題，才能那個決定極座標還是矩形座標哪個更有用。歐拉公式可以讓我隨意的進行轉換。同樣的e^ix 轉化為正餘弦函數，我們可以把任意的三角公式轉為以e表示的變量（這是很方便的——不需要去記憶sin(a+b)）。

從實用角度來看：每一種旋轉，每一種增長，甚至是每一個數字（複數或是虛數）都是e的變化，這真的很神奇。歐拉公式被認為是數學中最優雅的公示之一——而且確實可以理解其中的奧妙。