微積分導論

我對微積分真是既愛又恨：它既展示了數學的美，又體現出了數學教育中的痛苦。

涉及到微積分的話題都是很優雅的，而且很需要消耗腦力。我能想到的最接近的類比思想就是達爾文的進化論：一旦你想通了，你就會以一種從生存的角度看 待自然。你就會明白為什麼藥物會導致細菌的抗藥性（為了生存）。你知道為什麼糖和脂肪吃起來很美（在飢餓時候為了鼓勵進行高卡路里消耗）。這些都很符合進 化論。

微積分也有類似的啟人心智的作用。這些公式難道不應該有些關係嗎？

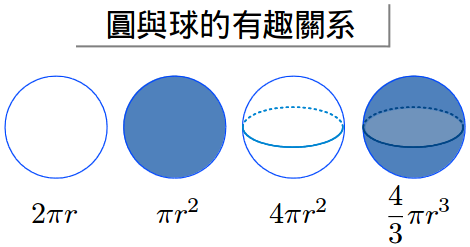
它們確實有，但是我們通常隻是單獨的去寫這些公式。微積分可以讓我們從「圓周長＝2π」開始就可以導出其他公式——即使是古希臘人也可以也可以推導出來。

不幸的是，微積分也可以作為數學教育問題的一個縮影。許多課程都是突出一些做作的例子，神秘的證明，記憶與抽象的符號操作，而這些還沒等我們掌握就已經關閉了我們的直覺化思維，並且打擊我們的學習熱情。

12.1 好吧小兄弟，你有什麼更好的主意？

不淡定了？我將不會做以下這些事：重新寫一些現存教科書已經有的東西。如果你需要這些東西來應付大型考試，那麼有大量的網站，班級，視頻還有其他一堆東西可以幫助你。

與此相反，我們將分享一些關於微積分的真正洞見。方程式並不夠——我希望有一些「醍醐灌頂」的時刻，可以瞬間明白其中的道理。

正式的數學描述隻是一種講述的方式而已。圖表，動畫，甚至是大白話也可以比滿頁的證明提供更多的深刻見解。

12.2 但是微積分很難

我覺得每個人都可以理解微積分。因為畢竟不是隻有作者才能理解莎士比亞的作品。

現在每個人基本上都懂得一些代數學與一般的數學嘗試。因為在不久以前，閱讀與寫作還僅僅是專業的書記員才能完成的。而現在即便是一個十歲的小孩子也可以進行閱讀與寫作。為什麼呢？

因為我們希望我們會，這種希望在「決定什麼事是可能」中扮演著重要的角色，希望對微積分懷有這種希望又是一個話題。有些人希望能深入到細節中去（作家/數學家）。但是剩下的我們完全可以隻關註發生了什麼就夠了，並且就此繼續下去。

這取決於你希望對微積分瞭解多深。我當然希望每一個人都能理解微積分的核心概念，並且能發出一聲驚嘆。

12.3 那麼微積分是關於什麼的呢？

有些定義說微積分就是「一個處理一個或多個變量的微分或積分或者是極限的函數的數學分支」。很正確，但是也幫不上菜鳥什麼忙。

這是我的結論：微積分就跟代數在算術上的地位一樣。

• 算術是關於操作數字的（加法，乘法等等……）
• 代數是發現數字間的規律：a² +b² =c² 就是一個著名的關係，描述了直角的兩個邊。代數幫你發現各種類型數字的集合——如果你知道a與b，然後就可以知道c了。
• 微積分幫助你發現方程式間的規律：你可以發現一個方程式（圓周＝2πr）與另一個類似的方程式（面積＝πr²）聯繫起來的。

使用微積分，我們可以解答以下問題:

• 方程式是怎樣增長與縮小的？經過一段時間它是如何積累？
• 什麼時候它達到最高點或最低點？
• 我們如何處理一直在變化的變量？（熱量，運動，人口……）
• 還有更多，更多！

代數與微積分是解決問題的二重奏：微積分發現新的方程式，然後用代數解決。就像進化論，微積分拓展你對自然的理解。

12.4 請舉一個例子

讓我們試試看。假設我們現在有一個周長方程（2πr），然後我們想找出面積方程。我們應該怎麼做呢？

你應該能發現一個光碟可以像是俄羅斯娃娃一樣嵌套起來的。

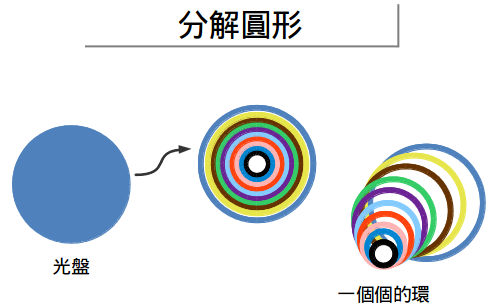
以下就是兩種畫出一個光碟的方法：

• 畫一個圓，然後把它塗滿
• 畫一堆圈然後把它們套在一起

兩種方法畫出來的面積應該一樣，對吧？而一個圈的面積是多大呢？

最大的圓的半徑應該是「r」，而周長就是2πr。越到裡面的圈，半徑越小，但是跟半徑始終保持2Π倍的關係。最小的圈應該像是一個點，它沒有周長。

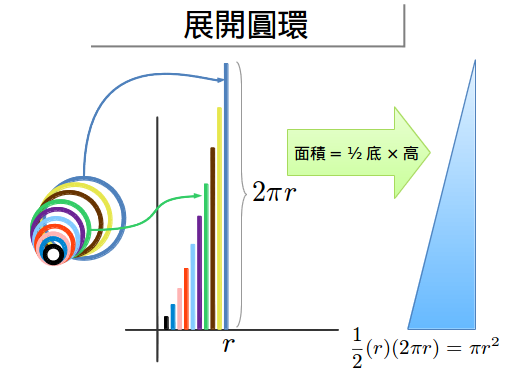
接下來事情就變得又去多了。讓我們把這些圈展開成直線，會發生什麼呢？

• 我們得到一堆線條，把它們組成一個鋸齒狀的三角形。但是如果我們把圈變得很細呢？這個三角形的鋸齒應該變得越來小。取得儘可能小以便達到更高的精確度是微積分的基本宗旨。
• 一邊有著最小的圈（0），而另一邊有著最大的圈（2πr）。
• 我們有著半徑從0到r的圈。取遍每一個可能的半徑，我們把它們放在對應位置。
• 「圈三角形的面積」＝底‧高/2＝r（2πr）/2＝πr² ，這就是圓的面積公式！

很棒！圈面積的和＝三角形的面積＝圓的面積！

這隻是一個簡單的例子，但是你明白其中的核心要點吧？我們取了一個光碟，然後把它分開，然後把碎片用另一種方法組合起來。微積分告訴我們一個光盤是如何與圈聯繫起來的：一個光盤就是一大堆圈。

這個主題再一次在為微積分中出現：大事物其實都是由小東西組成的。而有時候小東西更容易處理。

12.5 關於例子的一些提示

許多微積分示例都是基於物理的。這很棒，但是很難聯繫起來：說實話，你用物體的速度公式有多頻繁？一個星期也不不到一次吧。

我更喜歡使用客觀存在，可視化的示例來進行演示，因為我們的大腦就是這樣工作的。你可以親自使用紙片做一個圓盤，然後把它們剪開，然後拉直擺放成一個大概的三角形來看看是否真的可行。這可是在速度公式中辦不到的。

12.6 關於嚴謹的一些提示（針對數學專業）

我知道有些數學呆子可能都要把鍵盤扔向屏幕了。這是我關於「嚴謹」的一些看法。

你知道我們並不是以牛頓與萊布尼茨發現微積分時的方法去學習微積分的嗎？他們使用了「不斷的變化」（fluxions）與「極微小的」（infinitesimal）這些直觀化的概念而不是極限，因為「沒錯，實踐中這確實可行。但是在理論中是否一樣可行呢？」。

我們創造出了「嚴謹的」理論體系來證明微積分，但是卻忽略了我們直覺。

我們從腦化學的角度去看待糖，而不是根據自然天性去說「它有很多能量，我要吃掉它。」

我不想（也沒有資格）去教授分析課程或是培養研究生。但是讓普通大眾跟牛頓一樣用一種「非嚴謹」的方式去理解微積分有什麼不好？這可以改變他們看待世界的方式，同樣也改變了牛頓。

不合時宜的關註嚴謹會阻礙學生，同時也讓數學變得難學。舉個例子：e是通過極限定義的，但是它的發現確實通過對增長的直觀化觀察得到的。自然對數可以看作是積分，也可以看作是增長所需要的時間。哪種解釋更有可能幫助新手理解呢？

讓我們繼續沿著這條路隨手畫畫，然後發現其中的精彩之處。希望你能享受到快樂的數學。