指數函數與e

e經常讓我感到困惑——不是指這個個字母，而是指這個數學常量。它是個什麼東西呢？

數學書甚至是我深愛的維基百科都是用一種死板的專業術語來描述e：

數學常量e是自然對數的底。

當你去查詢自然對數時，你會看到如下的解釋：

自然對數，正式的名稱叫作雙曲線對數，是e的對數，而e是一個無理數，其值大約等於2.7182818248459。

很漂亮的循環引用。這就像辭典用拜占庭式的風格來定義迷宮一樣的風格一樣：正確但是並沒有什麼幫助。我們的常用詞彙有什麼問題呢？比如說“複雜的”。

我不是在挑維基百科的錯——為了追求它們的“嚴格”，許多數學解釋都是很乏味並且正式的，但是這並不能幫助初學者去能理解這些話題（我們都是或者曾是個初學者嘛）。

不要再這樣了！今天我就跟你們分享一下我關於e的直觀化的、更高層次的解釋，看看它是怎麼震撼你之前的認識的。以後再看你數學課本上的“嚴格”解釋吧

7.1 e不隻是一個數字

描述e就是“一個常數，它的值等於2.71828……”就像是說π是“一個無理數，它大概等於3.1415……”。是的，這樣說沒錯，但是你完全忽略了其中的意義。

Pi是所有圓的圓周與長其直徑的比。它是所有圓都具有的一個基礎性的比，因此它也廣泛適用於圓周長的計算，面積，體積還有圓球的表面積，球體，圓柱體等等。Pi很重要，不隻是與所有的圓有關，還有從中衍生出來的三角函數（Sin，Cos，Tan等）。

e是所有連續增長過程中所共有的基本增長量。e讓你在一個簡單的增長率中（這種增長每年底結算一次）發現連續的、復合計算的、在每分每秒甚至更短的間隔內一直增長的巨大影響，即使時每時每刻隻增長一點。

e出現在任何連續的進行指數增長的系統中：人口，放射性衰變，利息計算以及其他系統中。即使是在不連續的增長系統中也可以近似使用e來表示。

正如所有數字都可以看作是1（基本單位）的“倍數”那樣，所有圓也可以看作是一個單位圓（半徑為1）的“倍數”，所有的怎張都可以看作是e（一單位的增長率）的“倍數”。

所以e不是一個模糊不清的數字。e代表了所有連續增長的系統共有的一個增長率。

7.2 理解指數增長

讓我們先來看一個經過一段時間後正好翻倍的基本系統。舉例如下，

細菌可以進行分裂，而且每24小時就可以翻一倍。

我們每次把麵條對半一份就可以得到翻倍的麵條

如果你的錢可以收入100%的回報那麼它們每年就可以翻一倍（很幸運啊！）

它們看起來就像是：

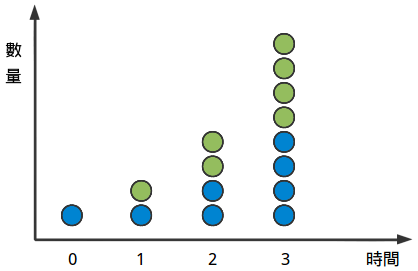
分成兩份或者是翻倍是一個很常見的過程。沒錯，我們可以翻兩倍或者是翻三倍，但是翻倍處理起來舒服些，我們先處理這個。

數學上，如果我們讓x分裂，那麼我們最後會得到2^x個多的“東西”。1分裂後我們可以得到2¹或2倍多的東西。4分裂我們可以得到2⁴＝16倍的東西。寫成方程式如下所示：

增長＝2^x

換言之，就是100%的增長率，我們可以把方程式寫成如下的形式：

增長＝(1+100%)^x

它們是完全等價的方程式，但是我們把“2”分開到底是什麼呢：原始的數值（1）再加上100%。很聰明吧？

當然，我們可以用其他數值（50%，25%，200%）來代替100%，那樣我們就得到了新的增長率公式。所以更一般的方程式可以寫成：

增長=(1+增加的部分)^x

這就是說我們把（1+增長的部分）自乘了x次。

7.3 更詳細的探討

我們的公式假設我們的增長髮生在一定的間隔之後。細菌在等待，等待，然後就激增，它們在最後一分鐘翻倍了。我們的利息就在一年的時候突然就有了。根據以上的公式，增長是間斷的，然後瞬間就增長了。那些綠的點突然就冒出來了。

但是真實的世界並不是這樣的。如果我們放大查看的話，我們就會發現我們的細菌朋友每時每刻都在增長：

綠色先生並不是突然出現的：他從藍色先生中慢慢成長起來，經過一單位時間後（在這個例子中是24小時），綠色先生完全長大了，它成了一個完整的藍色先生，然後它又接著生出了它自己的綠色細胞。

這個細節改變了我們的方程式了嗎？

沒有。在細菌的例子中，處於一半形態的細菌還什麼都不能做，直到它們完全長大，並且脫離了它們的父母。方程式仍然適用。

7.4 有錢能使鬼推磨

但是對於錢來說就不一樣了。我們可以馬上賺到5毛錢的利潤（譯者在這裏做了惡搞修改，放心，這不會影響討論^_^），這個5毛可以產生自己的5毛。我們不需要等到有了1元的利息後再產生新的利息——新錢不需要老錢來生成。

根據我們之前的方程式，利息的增長看起來應該是這樣的：

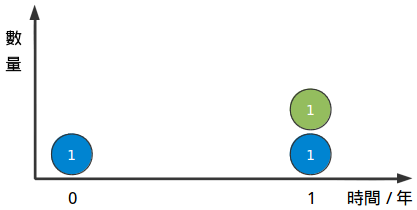
但是再一次的，這也不是很准確：所有的利息都是直到最後一天才出現的。讓我們把它放大，然後把一年分為兩半。我們每年都賺到100%的利息，也可以說我們每六個月賺到50%的利息。那麼，我們前半年賺5毛，後半年又賺5毛：

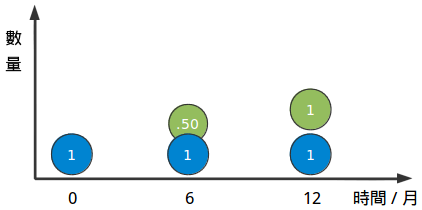
但是這樣還是不准確！是的我們原來的一元（藍色先生）經過一年後又賺了一元。但是半年後我們又有了五毛，准備好了，我們忽略了一部分！那就是那個五毛也可以產生自己的利潤：

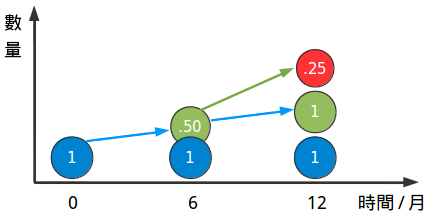
因為我們的增長率是每半年增長50%，那麼那個五毛可以賺到0.25元（5毛乘以50%）。一年之後我們就有：

我們最開始的一元錢（藍色先生）

最開始的一元錢賺到的錢（綠色先生）

還有綠色先生賺到的0.25元（紅色先生）

總共有2.25元。我們從我們最開始的錢中賺到了1.25元，比翻倍還要多！

用公式表達出來，按照50%計算的兩段時間內的增長率是：

增長＝(1+100%/2)²=2.25

7.5 繼續深入到復合增長率中

是時候讓我們更進一步了。不再是把增長分在兩個時期中，其中各50%，讓我們把它分成3份，每份33%的增長率。誰說我們隻有等到半年後才能開始獲得收益？讓我們把它們分得更細一些。

用圖表把這個表示出來就很有趣了：

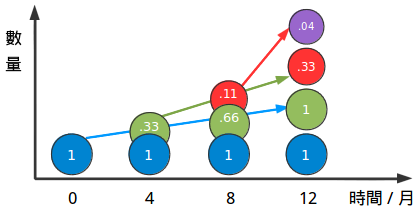
把每種顏色當作一部分另一種顏色所生的孩子，1/3的時間內：

剛開始時：我們從藍色先生開始，我們隻有1元錢

第四個月：藍色先生賺到了1/3的錢，而且它生出了綠色先生，有0.33元。

第八個月：藍色先生有賺到了0.33元給了綠色先生，綠色先生現在又0.66元，綠色先生這時也賺到了0.11元，這就是紅色先生。

第十二個月：情況開始變得更複雜了。藍色先生又賺了0.33元給了綠色先生，綠色先生現在正好有1元錢。而綠色先生也賺了0.22元，現在紅色先生總共有0.33元，而紅色先生最開始有0.11元，現在它也賺了0.04元，這就是紫色先生了。

嗖！經過一年後，最後我們有：1+1+0.33+0.04，大概有2.37元。仔細想想這是怎麼發生的吧：

每個顏色都產生自己的利潤，並把它交給另一種顏色。新的顏色在下一個週期便可以產生自己的利潤。

我喜歡把最開始的錢當作始終沒有變化。藍色部分產生錢給綠色先生，每四個月固定產生0.33元給綠色先生。在圖表中有個箭頭表示藍色先生是怎樣把錢給綠色先生的。

綠色先生把自己產生的錢給了紅色先生，而這其中沒有藍色先生的貢獻。

隨著時間的增加，綠色先生也在增長（而藍色先生一直保持不變），他給紅色先生越來越多的錢。在第四個月到第八個月之間，綠色先生給了紅色先生 0.11元，而在第八個月到第十二個月之間，綠色先生有.66元，所以它給了紅色先生0.22元。把圖表展開，綠色先生總共給了紅色先生0.33元，而綠色先生則擁有整整一元錢。

明白了吧？剛開始時可能難以理解——我把圖表整合在一起時自己甚至也有些迷糊了。但是明白了每部分錢產生自己的錢，然後它們又產生自己的錢，如此週而復始，我便明白了。

分為3個週期後我們就可以得到如下的增長方程式：

增長＝(1+100%/3)³=2.37037……

我們賺到了1.37元，比之前的1.25元更多！

7.6 我們可以賺到無限多的錢嗎？

為什麼不取更小的時間間隔呢？如果換為每個月，每天，每小時，甚至是每個毫微妙呢？我們會馬上稱為億萬富翁嗎？

我們的收入會增加，但是會達到一個固定的點。試著把之前的方程式換成其他的值，看看結果：

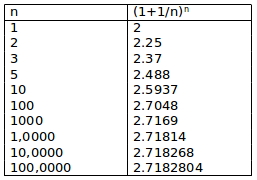
數字變得更大，但是最終會集中在2.718附近。嘿……等等……這個好像就是e啊！

沒錯！用專業術語表示就是，e是在足夠小的時間間隔內按照100%復合增長的增長率：

$e = \lim_{n \to \infty}\Big(1+\frac{1}{n}\Big)^n$

這個極限最終將集中在一個點，這個可以進行證明。但是正如你所看到的，我們可以取更小的數字來發現它確實集中在2.718附近。

7.7 這又意味著什麼呢？

數字e（2.718……）代表了在一段時間內按照100%進行復合增長所能達到的最大增長率。沒錯，當初你隻是期望從1增長到2而已。但是每一小步，你所創造的收益又會產生自己的收益。當這些結束後，你在一段時間內從1增長到了e（2.718），而不是2.

那麼，如果我們從1開始以100%進行復合增長，那麼我們將得到1e。如果我們以2開始就得到2e，以11.79開始就得到11.79e。

e就像是最高時速限制（就像光速c），告訴我們在一個連續的復合增長中所能達到的最快速度。

7.8 如果是不同的增長率呢？

問得好！如果我們每年增長50%而不是100%呢？我們還能適用e嗎？

讓我們看看。50%的復合增長會是這樣：

$\lim_{n \to \infty}\Big(1+\frac{0.50}{n}\Big)^n$

我們可以怎麼做呢？好吧假設50%分為了50份：

$\Big(1+\frac{0.50}{50}\Big)^{50} = (1+0.01)^{50}$

沒錯，這個並不是無限的，但是也夠多了。假設我們把通常的100%的增長分為1%大小：

$e \approx \Big(1+\frac{1.00}{100}\Big)^{100} = (1+0.01)^{100}$

啊哈，有些東西在這裏融為一體了。在我們的一般例子中，我們等於是把1%累加了100次，在50%的案例中，我們把1%累加了50次。

這兩個數字間有什麼區別呢？好吧，隻是改變了一半而已：

(1+0.01)⁵⁰=(1+0.01)^100/2=((1+0.01)¹⁰⁰)^1/2=e^1/2

這就很有趣了。50/100＝0.5，而e的指數正好也是0.5.推廣到一般情形：如果我們的增長率換為300%，我們就可以把300%分為1%一份。最後我們就會得到e³。

即使增長率看起來像加法（+1%），但是我們必須切記它其實是乘法（×1.01）。這就是為什麼要使用指數（連續的自乘）以及平方根（e^1/2就是說隻改變了一半，舉例來說就是一半的乘法）

即使我們選擇1%，但是我們還可以選擇其他更小單位的怎張（0.1%，0.00001%甚至是無窮小！）關鍵在於無論我們取何值，都隻是e有一個新的指數而已。

7.9 如果是不同的時間間隔呢？

假設我們300%的增長在兩年後是多少呢。我們把每年的增長乘以它自己便得到：

增長＝(e³)²=e⁶

更一般化的表示就是：

增長＝（e^增長率）^時間＝ e^{增長率·時間}

因為神奇的指數，我們避免了處理冪而直接在指數中把增長率與時間相乘就可以了。

7.10 玄機：e使增長率與時間結合在一起

這很瘋狂！e^x可以把它們合並在一起：

x就是我們計算增長的時間：每年增長100%，3年後就是e³

x就是增長率：一年增長300%就是e³

這個不會讓它倆發生混淆嗎？我們的方程式會失效，世界會毀滅嗎？

它們完全可以在一起，當我們寫下：

e^x

x其實就是增長率與時間的組合：

x＝增長率·時間

讓我解釋一下。處理復合增長時，每年增長3%，增長十年與一年增長30%的效果一樣，不考慮之後的效應。

每年增長3%，增長10年。就是說1%纍計了30次。這些變化發生在十年的時間內，每年連續增長3%。

一年增長30%，也是說1%纍計了30次。隻不過是發生在一年之內，一年就改變了30%。

每個例子其實都是說“1%纍計了30次”。你的增長率越大所花費的時間越少，增長率越小，你所花費的時間越長。

但是在兩個例子中，最終的增長率都是e^0.3＝1.35。我們更傾向於在短時間內獲得更大的增長，但是e告訴我們，其實它們都一樣。

所以，我們的公式變為：

增長＝e^x＝e^r·t

如果我們在時間t內的增長率是r，那麼我們的凈增長就是e^r·t。即使是對負數與分數，這個公式依然成立。

7.11 示例時間

示例讓許多事情變得更有趣。小提示：我們通常喜歡使用2^x或其他常規的式子，遇到復合增長感到困惑其實很正常（包括我在內）。稍後我們將遇到各種簡單的連續復合增長的例子。

這些例子都是指連續的平滑增長，而不是“跳躍性”的增長，比如說按年增長。可以把它們進行轉化，但是這不是這裏所要討論的。

示例1：寶石生長

假設我有一個300Kg的魔力寶石。它們之所以被稱作魔力寶石是因為它們每天都在生長：一個寶石，經過一天之後，會產出一個跟它重量相等的寶石。而新的寶石剛一產出就開始生長，但是我不可能追蹤這些細節——我更關註最開始的那個寶石能生出多少寶石。十天之後我有多少呢？

首先這是一個相當需要技巧的例子：我們的每天的增長率是100%，而我們想知道10天之後的復合增長率是多少。每個寶石隻知道100%（“每過24小時我要產生一個與自身重量相等的寶石”），而最終復合增長有多少（“那些寶石是你生出來的？呃，是它們自己生出來的”）

e就是那個神奇的變化因子：每天增長100%，那麼十天之後就有：300·e^1·10＝660萬多公斤寶石。

在大多數情況下，我們通常不知道最開始的基本增長率是多少（e^100%，距離來說，我們紙知道一天之後1個寶石變為2.718個寶石），但是使用自然對數ln我們可以推出最初的增長率（這個例子中為100%）。

示例2：最大利率

假設我有120元，按照5%的利率計算。我的銀行很慷慨，給了最大的復利。10年之後我能賺多少錢呢？

利率是5%，而我很幸運可以連續計算復利。十年之後，我就有120·e^0.05·10＝197.85。當然，大部分銀行不可能給你這麼好的福利。你實際的收入與你想像的連續收入的差別取決於他們有多不喜歡你。

示例3：放射性衰變

我有10公斤的放射性物質，它們每年都以100%的速度進行連續性衰變（這就是說，每年它們都要10公斤每年的速度進行衰變），3年後我還有多少呢？

0？沒有了？再想想。

我們剛開始的速度是每年100%，是的，我們剛開始有10公斤，然後預期一年後它將一點不剩。

但是猜猜這個：幾個月後，我們有5公斤。還剩下多少時間呃？從我們以“10公斤每年”開始後還有半年。

不是！我們現在有5公斤，我們現在的速度是5公斤每年，所以我們從現在開始還有整整一年呢！

再過幾個月等到它衰變到2公斤後。看看會發生什麼呢？我們的衰變速率變為2公斤每年，所以我們接下來又有整整一年。剩下1公斤時，我們又有一年，剩下0.5公斤時我們又有一年——看到其中的規律了嗎？

隨著時間的流逝，我們的物質發生衰變，但是衰變的速率也在減少。這個持續變慢的衰變過程就是持續復合增長的方面。

3年後，我們還有10·e^-1·3＝0.498公斤。正如我們所看到的我們在衰變中使用了一個負指數：

負增長率（減少）。負指數就等於給了一個分數（1/e^r·t）來減少

負時間。一個負指數就像是讓時間倒流；不再是看10如何增長到0.498，而是看10如何變回0.498

負指數就是另一種改變：不再是增長而是減少。

7.12 還有更多東西需要去學習

我的目標就是：

解釋e為什麼很重要：這是一個基本常數，就像π一樣，它告訴我們關於增長的東西。

給出一個直觀化的解釋：e讓你看到各種不同增長率所產生的影響。即使是新的部分（綠色先生，紅色先生等等）也可以在總增長中做出自己的貢獻。

展示它是如何應用的：e^rt 讓我們可以預測各種增長率在不同時間段內的增長。

讓你產生繼續學習的興趣：在接下來的章節中我會向你們展示更多關於e的性質

這隻是一個開始——在一個章節中填充太多東西會讓你我都感到很累。除去身上的灰塵，休息以下，准備學習e的邪惡雙胞胎，自然對數吧。

飲水思源

《更好的解释（数学篇）》——第七章