發掘數學直覺

我們的第一印象塑造了我們的對概念的直覺。而我們的直覺直接影響了我們有多喜歡它。我在說什麼呢？

假設我們想定義“貓”這個概念：

• 洞穴人的定義：一個有著爪子，牙齒，尾巴，四條腿的毛茸茸的動物。它高興時會嗚嗚叫，生氣時則發出嘶嘶聲……
• 進化論版的定義：哺乳動物的後裔，隸屬於貓種，擁有相同的特徵。
• 現代的定義：你稱這些是定義？貓是一種動物，它們的DNA為：ACATACATACAT……

現代的定義當然是最准確的了，這點毫無疑問。但是它是最好的定義嗎？你就是這樣教一個小孩子去學習這個單詞的？這個定義真的深刻的揭示了貓這種動物嗎？不見得。現代的定義是有它的用處，但是是在獲得了對貓的認知之後的才有用。這不應該是我們的起點。

不幸的是，理解數學很多時候就像理解DNA一般。我們被教授給了現代的，十分嚴謹、細密的定義，但是並沒有能夠深刻的洞察它的由來。我們隻是知道了一堆神秘的方程式（DNA），但是卻完全不明白它到底是什麼。

讓我們從不同的角度接近一個概念。我想像了一個圓：圓心是你要學習的概念，而它的四週則是各種描述它的事實。我們從一個角落開始學習，僅僅依靠一個 事實或是見解，然後不斷的加深我們的理解。貓都有共同的物理特徵，所以貓有一個共同的祖先，因而一個特定的物種可以通過特定的DNA進行區分。啊哈 （Eureka也行啊——譯者註）！我們現在知道貓的定義是怎樣從洞穴人的定義進化到現代的定義了。

但是並不是所有的開始都是一樣的。正確的開始可以讓我們更快、更好的理解數學——而數學中那些首先發現定理（或者公理之類）的洞穴人通常都有啟髮式的觀點（Enlightening Viewpoint）。接下來就讓我們學習一下如何構建我們的直覺吧。

1.1 圓是什麼？

我們來舉一個數學例子：我們該如何定義一個圓呢？

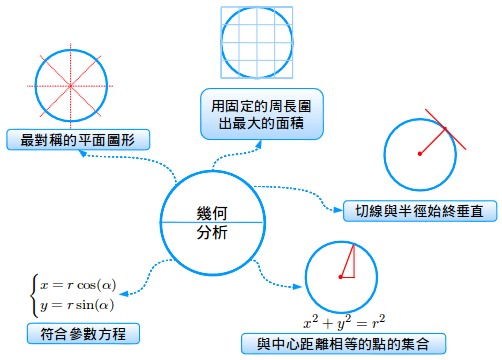
看上去好像有無數多個定義，這裏舉一些例子：

• 對稱度最高的二維圖形
• 用最少的周長圍出最大面積的圖形（等周圖形性質）
• 平面上距離給頂點相等的點的集合（用圓規或帶弦的鉛筆即可畫出）
• 點（x,y）滿足方程x² +y² = r² (根據幾何上的解析定義)
• 符合參數方程r*Sin(t),r*Cos(t),對所有的t取值（真正的解析定義）
• 切線始終與位矢向量垂直的圖形（物理解釋）

這個列表還可以繼續補充下去，但是有一個關鍵點：它們都描述了同一個概念！這就像說1，一，首（1，one，uno，eins） ，“2x+3＝5的解”“你臉上鼻子的個數”——它們隻是同一個概念的不同名字而已。

但是這些初始的描述很重要——它們決定了我們的直覺。我們先在生活中見到了圓然後才在課堂中學習它，我們明白它們“圓”。不管是怎樣令人驚艷的方程式（x² +y² = r² ），我們都深刻得知道圓圈是圓的。如果我們根據方程畫出了圖形，但是圖形是方的或是不對稱的，那我們便知道其中必然有問題。

小孩子，就像洞穴人一樣學習圓的定義（就是個很圓的東西），這給了我們一個很直觀的感覺。我們可以發現在圓的東西上，每一個點距離中心都是相等的。x² +y² = r² 就是用解析的方法描述這一事實（利用畢達哥拉斯理論的距離表示法）。我們從一個點出發，根據我們的直覺，然後推導出了正式的定義。

其他概念就未必有如此幸運了。我們能夠憑直覺瞭解到e的增長率嗎，還是它是一個抽象的定義？我們能瞭解i的旋轉嘛，還是它隻是一個人造的，沒用的概念？

1.2 構建直覺的策略

現在我仍然需要時不時得提醒自己e與i的深層含義——這就像需要提醒自己記住“圓圈是圓的”或“貓是什麼樣子的”一樣荒唐！我們開始學習它時就應該是自然而然的一件事。

忽略了重點經常讓我抓狂：數學就是有關概念的——方程式隻是一種表達的方式而已。一旦清楚了中心要點，方程式很快就可以建立起來。這裏是一些幫助過我的策略：

步驟1：發現數學概念的中心要點。 這可能會比較難，但是試著從它歷史開始學起。這個概念第一次出現在哪裏呢？發現者做了哪些工作呢？之前的用法可能會區別於現在的解釋與應用。

步驟2：通過用一個話題來解釋一個性質或事實。用一個話題來模擬正式的定義。如果幸運的話，你可以把數學方程（x² + y² = r² ）翻譯成大白話（“距離中心都相等的點的集合”）

步驟3：使用相同的話題來探索相關的性質。一旦你通過以上的工作有了一個類比或解釋，試試看它能不能用到其他性質中去。有時可以，但有時不行（這時你就需要一個新的理解了），但是對你所發現的東西必然會感到大吃一驚。

讓我們試一試吧。

1.3 一個實例：理解e

理解數字e是一項重要的工作。e在出現在各種科學中，而且它有多重定義，但是沒有一種能讓人們自然而然的理解它。讓我們就這個概念發掘一些本該有的 直覺。接下來將會有幾個簡單描述這個概念的方程式。即使這些方程式看起來莫名其妙，但是背後都有著大白話的描述。以下就是關於e的幾種定義：

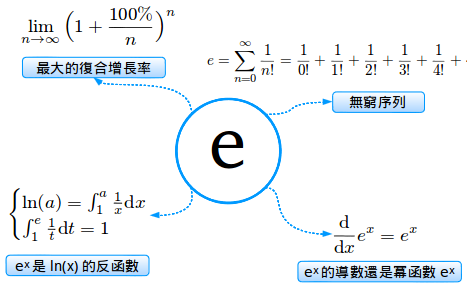
第一步就是要發現一個話題。回顧e的歷史，它好像是與增長率或利率有關的。e是在進行商業計算時發現的（而不是抽象的數學推測），所以個“利息”（增長率）就是一個合適的話題。

讓我們看看它的第一個定義，在圖中左上方。對我來說，最關鍵的跳躍是，認識到關於復利計算的公式到底會有多大。事實上，這是你按照盡可能短的週期，以100%的利率計算復利所能達到的值。這就描述了這樣一個關於e的定義。

定義1：e就是按照100%的復合增長率，以盡可能小的週期計算復利所能達到的值。

---

接下來讓我們看看第二個定義：是一個無窮序列，後面的數值變得越來越小。這是什麼呢？

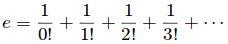
利用“利率”這個話題我們來處理這堆式子。我們發現這是復利的組成部分。現在它的深層含義不是那麼直觀——但是我們思考一下在討論增長率時，“1+1+1/2+1/6 …”代表了什麼？

首先，第一個代數項（1＝1/0!，記住0!等於1）是你的本金，最開始的資金。然後第二個代數項（1＝1/1！）是你直接賺得的利息——1的 100%。接下來的代數項（0.5=1/2!）是你利息所賺得的利息（第二級利息）。接下來的代數項（0.1666=1/3!）是你的第三級利息——就是 你的利息的利息所賺得的利息。

錢生的錢又可以生錢，而生下來的錢又可以繼續生錢，如此無窮無盡——這些無窮無盡的序列做出了各自的貢獻（這樣的描述表明，張三，李四都是獨立長大，互不相幹）。還有很多東西可以說，但是讓我們集中在增長率上來理解這個概念吧。

定義2：e就是各個利息自己的貢獻之和。

---

目前為止非常成功。接下來搞定第三個定義。它代表什麼呢？不如想想“導數”（這將把你的大腦調節到方程式模式），想想它代表什麼。對方程式的感覺。讓它成為你的朋友。

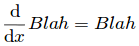
這是用微積分的方法表示“你的增長率等於你現在的數值”嗯，增長率等於你現在的數值就表示是100%的利率，對吧？而它一直在增長就意味著你需要一直計算利息——這是另一種描述連續的復合增長率的方法！

定義3：e就是一個按照100%的倍率在增長的數。

很好——e就是一直完全按照自身的大小在增長的數，而不是1%或200%。

---

輪到最後一個定義了——它相當棘手。這是我的解釋：之前一直在談論你收入了多少錢，現在為什麼不談談增長到一定數值需要畫多長時間呢？

如果你現在是1，然後按照100%的倍率增長，這將花去一個單位時長從增長到2。但是一旦你達到2，然後接著增長一倍，這意味著你每個單位時長可以增長兩倍！所以你隻需花去半個單位時長即可從2增長到3。從3增長到4隻需花去1/3單位時長，就這樣計算下去。

從1增長到A所需要花費的時長是從1到2，從2到3，從3到4……一直進行下去直到A總共所需要花費的時長。利用第一個定義很自然就可以從“增長所耗的時間”的計算中定義“自然對數（ln）”。

ln(a)就是從1增長到a所需要花費的時間。然後我們就知道e就是花費一單位時長可以增加多少。換言之，e就是一單位時長後所增長的部分！

定義4：定義連續的從1增長到ln(a)所花的時間。e就是經過一單位時長後所增加的部分。

哇哦！這就是關於神秘的e的四種描述方式。一旦我們直到了核心概念（“e就是關於一倍的連續增長”），再複雜的方程式也是那麼自然而然——這就可以把微積分用大白話翻譯出來，因為數學就是關於概念的。

1.4 這其中寓意著什麼？

在數學課堂上，我們經常從最新的，最複雜的概念開始學起。因此我們感到困惑並不意外：我們向學生展示DNA，然後期望他們能看到一隻貓。

我從這種方法中學到了不少東西，而這直接影響了我如何理解與解釋數學：

• 探索其中的要義並應用它們。最初的直覺除了可以幫助我們洞察所有事，還可以幫我們明白它為什麼在那裏。從一個有意義的定義開始，然後不斷的在周邊探索它。
• 學會利用資源。生硬的去理解概念沒有一點樂趣。如果沒能茅塞頓開，換一個角度試試。總有另外一本書，另外一篇文章，或另外一個人可以幫助你理解。
• 形象化挺好的。我們認為數學是嚴格的，解析的。——但是形象化的解釋也是可以的！儘管利用能幫助你理解的方法。虛數就一直讓人迷惑，直到發現了它們的幾何解釋，這都距離發現它們好幾十年了。整天盯著公式看並不能幫助你明白它們到底是什麼。

如果我們看重定義而忽視理解，那麼數學會很難而且會讓我們狠受打擊。記住現在的定義是十分高級並且先進的想法，但並不是一定要從這裏開始。不要害怕從一些可笑的角度開始接近它——整出方程式背後的大白話。學習數學就會變得很快樂。